定义
假设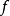 是定义在区间
是定义在区间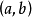 上的函数,如果下列准则成立:
上的函数,如果下列准则成立:
任意给定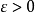 ,能够找到
,能够找到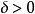 ,使得满足不等式
,使得满足不等式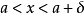 的一切
的一切 ,恒有
,恒有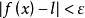 。
。
则称当 由右边趋于
由右边趋于 时,收敛于极限
时,收敛于极限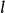 。记为
。记为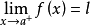 。
。
数值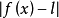 是
是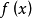 与
与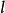 之间的距离,我们可以认为它是用
之间的距离,我们可以认为它是用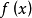 近似表示
近似表示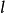 所产生的误差。因此
所产生的误差。因此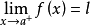 的定义,相当于断言:用
的定义,相当于断言:用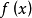 近似表示
近似表示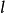 所产生的误差可以小到我们任意指定的程度,只需要
所产生的误差可以小到我们任意指定的程度,只需要 从坐标充分靠近
从坐标充分靠近 。1
。1
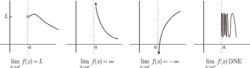
性质左极限与右极限统称单侧极限。
①函数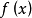 当
当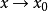 时,极限存在,当且仅当函数
时,极限存在,当且仅当函数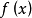 在
在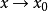 处
处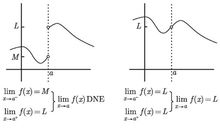 左极限和右极限都存在,且两者相等。用数学表达式表示为:
左极限和右极限都存在,且两者相等。用数学表达式表示为:
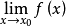 存在
存在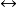
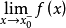 和
和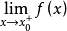 都存在且
都存在且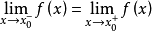 。
。
②函数的左极限和右极限不一定相等,例如:
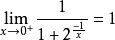
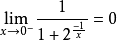
此时称函数在该点有“跳跃”。
③左极限与右极限只要有其中有一个极限不存在,则函数在该点极限不存在。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国