[科普中国]-波莱尔集

简介

在数学中，对波莱尔集的研究主要是在描述集合论中。但是，大学数学系的学生通常是在实变函数论的课程中最早接触到波莱尔集。1

波莱尔集可以分成很多的层次。通常把开集和闭集定义为第一层。可数的开集的交集，可数个闭集的并集为第二层。依此类推，总的层次超过了可数层。

波莱尔集是由开集或闭集通过取并，取交或者取补形成的拓扑空间中的任何集合。

对于拓扑空间X，X上的所有波莱尔集的集合形成σ-代数，称为波莱尔代数或波莱尔σ-代数。 X上的波莱尔代数是包含所有开集（或所有闭集）的最小σ-代数。

波莱尔集在测度论中是很重要的，因为任何度量都在该空间上的开集和闭集以及波莱尔集上定义。在波莱尔集上定义的任何测度都被称为波莱尔测度。 波莱尔集和相关的波莱尔层也在集合理论中发挥关键性作用。

在某些情况下，波莱尔集被定义为由拓扑空间的紧集而不是开集生成。这两个定义对于许多空间（包括所有豪斯多夫σ-紧集）来说是等价的，但在病态空间中可以是不同的。2

生成波莱尔代数在X是度量空间的情况下，波莱尔代数的第一意义上可以被描述如下：

对于X的子集的集合T，让：

（1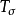） 都是T的元素的可数集；

（2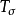） 是T的元素的所有可数交集；

（3） 。

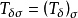现在通过下列方式来定义序列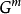 ，其中m是序数：

（1）对于定义的基本情况，让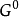 是X的开放子集的集合。

（2）如果i不是一个极限序数，那么i有一个紧接在前面的序数i-1，让

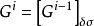
（3）如果i是一个极限序数，让

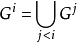
波莱尔代数是Gω1，其中ω1是第一个不可数序数。 也就是说，波莱尔代数可以通过迭代运算到第一个不可数序数从开放类生成。

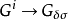
为了证明这种说法，请注意，度量空间中的任何开集是闭集的递增序列的并集。 特别地，集合的互补将Gm映射到极限序数m；此外，如果m是不可数的序数，Gm在可数集合下封闭。

注意，对于每个波莱尔集合B，存在一些可数序数αB，使得可以通过迭代αB上的操作来获得B。 然而，随着B在所有波莱尔集上变化，αB将在所有可数序数上变化，因此获得所有波莱尔集的第一个序数是ω1，第一个不可数的序数。3

举例（1）有一个很重要的例子，特别是在概率论中，是实数集上的波莱尔代数。 它是一种波莱尔测度被定义的代数。 给定在概率空间上定义的真实随机变量，其概率分布也是波莱尔代数上的度量。

（2）雷达上的波莱尔代数是包含所有间隔的R上最小的σ-代数。

（3）在通过无限次感应的构造中，可以看出，在每个步骤中，集合的数量最多是连续体的数量。 因此，波莱尔集合的总数小于或等于

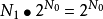
标准波莱尔空间和库拉托斯基定理让X是拓扑空间。 与X相关联的波莱尔空间是一个对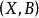：，其中B是X的波莱尔集的σ-代数。

麦克定义了一个不同的波莱尔空间，写出它是“与一个被称为它的波莱尔集的子集的σ-域”。然而，现代用法是将可分辨的子代数可计量集合和这样的空间称为可测量空间。 这个区别的原因是波莱尔集是由开集（拓扑空间）生成的σ-代数，而麦克的定义是任意σ-代数的集合。 存在可测量的空间，而不是波莱尔空间。

可测量空间形成一个类别，其中态射是可测量空间之间的可测量函数。 函数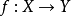是可测量的，如果它拉回可测量集合，即对于Y中的所有可测量集合B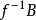，是X中的可测量集合。

定理：令X为波兰空间，即拓扑空间，使得X上的度量d定义X的拓扑，并使X成为完全可分的度量空间。那么X作为波莱尔空间与（1）R、（2）Z或（3）有限空间之一是同构的。 （这个结果让人想起马哈拉姆定理）

被认为是波莱尔空间，实线R，R与可数集的并，以及Rn他们是同构的。

标准波莱尔空间是与波兰空间相关联的波莱尔空间。标准的波莱尔空间的特征在于它的基数同构，和任何不可数的标准波莱尔空间具有连续体的基数。

对于波兰空间的子集，波莱尔集可以表征为这些集合，其是在波兰空间上定义的连续注入图的范围。但是请注意，连续非投影地图的范围可能无法为波莱尔。

在标准波莱尔空间上的每个概率测量将其变为标准概率空间。4

替代的非等效定义根据P.Holmos所描述的，局部紧凑豪斯多夫拓扑空间的子集称为波莱尔集，如果它属于包含所有紧集的最小σ-环。

诺伯格和Vervaat将拓扑空间X的波莱尔代数重新定义为由其开集及其紧集的饱和子集产生的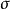-代数。 在X不是豪斯多夫的情况下，此定义非常适合。 如果X是第二个可计数的，或者每个紧集的饱和子集是封闭的（特别是X是豪斯多夫）的情况下，它与通常的定义一致。