[科普中国]-旋转法

背景

当空间几何元素对投影面处于一般位置时，它们的投影一般不反映真实形状和大小，也不具有积聚性，但当它们对投影面处于特殊位置时，则其投影反映真实形状和大小，同时，也具有积聚性。当图示、图解一般位置的空间几何元素及其相互间的定位和度量问题时，如能把它改变成特殊位置，则问题就可能比较容易地获得解决。投影变换的方法可以达到上述目的。典型的投影变换方法有正投影变换和斜投影变换。正投影变换用改变几何元素与投影面体系的相对位置来达到投影变换的目的；斜投影变换保持投影面和空间几何元素的位置不动，改变投射方向(即采用斜投影)，使空间几何元素在投影面上的新投影有利于解题。其中，正投影变换包括变换投影面法(换面法)和旋转法。变换投影面法保持几何元素的位置不动，而建立新的直角投影面体系；旋转法保持原直角投影面体系不动，将空间几何元素绕某个选定的轴旋转。

分类如图1所示，空间点A绕直线OO旋转，点A称为旋转点，直线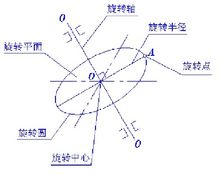OO称为旋转轴。自A点向OO轴引垂线，其垂足O称旋转中心，AO称旋转半径，A点的旋转轨迹是以O为圆心，以AO为半径的圆周，称为轨迹圆，轨迹圆所在的平面与旋转轴垂直。

按旋转轴对投影面的相对位置，旋转法分为：

（1）绕垂直于投影面的轴线旋转----垂直轴旋转；

（2）绕平行于投影面的轴线旋转----平行轴旋转；

（3）绕一般位置轴线旋。

点的旋转如图2所示，点A绕垂直于V面的OO轴(正垂轴)旋转，其V投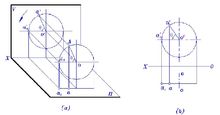影反映轨迹圆实形，而H投影为过A点且平行于X轴的直线段，其长度等于轨迹圆的直径。

如图3所示，点A绕铅垂轴旋转，其H投影反映轨迹圆实形，即H投影a沿圆周旋转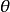角到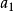，其V投影a’沿投影轴的平行线移动至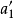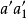，//OX。

由上可知点的旋转规律为：当点绕垂直轴旋转时，点在与旋转轴垂直的那个投影面上的投影作圆周运动，而另一投影则沿与旋转轴垂直的直线移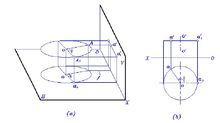动。

直线的旋转直线的旋转，仅需使属于该直线的任意两点遵循绕同一轴、沿相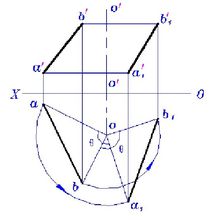同方向、转同一角度的规则作旋转，然后，把旋转后的两个点连接起来。

如图4所示，直线AB绕铅垂轴OO按逆时针方向旋转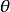角，也就是使A、B两点分别绕OO轴逆时针旋转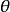角，按照点的旋转规律求得、。

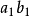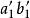直线旋转的基本性质为：

（1）直线绕垂直轴旋转时，直线在旋转轴所垂直的投影面上的投影长度不变。

（2）直线对旋转轴所垂直的那个投影面的倾角不变。

（3）直线在旋转轴所平行的投影面上的投影长度及对该投影面的倾角都改变。

平面的旋转平面的旋转是通过旋转该平面所含不共直线的三个点来实现的，旋转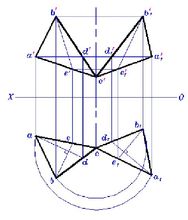时，必须遵循同轴、同方向、同角度的规则。

平面的旋转性质为：

（1）平面绕垂直轴旋转时，平面在旋转轴所垂直的投影面上的投影，其形状和大小都不变。

（2）平面对旋转轴所垂直的那个投影面的倾角不变。

（3）平面的另一个投影，其形状和大小发生改变，并且，该平面对旋转轴所不垂直的那个投影面的倾角也改变1。