历史发展问题的起源
达·芬奇不仅是意大利的著名画家,他画的《蒙娜丽莎》带给 了世界永恒的微笑,而且他还是数学家、物理学家和机械工程师,他学识渊博,多才多艺,几乎在每个领域都有他的贡献,他还是数学上第一个使用加、减符号的人,他甚至认为:“在科学上,凡是用不上数学的地方,凡是与数学没有交融的地方,都是不可靠的”。他本人在创作《蒙娜丽莎》时,认真地研究了主人公的心理,做了各种精确的数学计算,来确定人物的比例结构,以及半身人像与背景间关系的构图问题。当我们欣赏着他的《抱银貂的女人》中脖颈上悬挂的黑色珍珠项链时,我们注意的是项链与女人相互映衬的美与光泽,而不会像达·芬奇那样去苦苦思索这样一个问题:固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?
了世界永恒的微笑,而且他还是数学家、物理学家和机械工程师,他学识渊博,多才多艺,几乎在每个领域都有他的贡献,他还是数学上第一个使用加、减符号的人,他甚至认为:“在科学上,凡是用不上数学的地方,凡是与数学没有交融的地方,都是不可靠的”。他本人在创作《蒙娜丽莎》时,认真地研究了主人公的心理,做了各种精确的数学计算,来确定人物的比例结构,以及半身人像与背景间关系的构图问题。当我们欣赏着他的《抱银貂的女人》中脖颈上悬挂的黑色珍珠项链时,我们注意的是项链与女人相互映衬的美与光泽,而不会像达·芬奇那样去苦苦思索这样一个问题:固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?
这就是著名的悬链线问题,达芬奇还没有找到答案就去世了。
发展从外表上看,悬链线真的很像抛物线。荷兰物理学家惠更斯用物理方法证明了这条曲线不是抛物线,但到底是什么,他一时也求不出来。直到几十年后,雅各布·伯努利再次提出这个问题。
解决问题与达芬奇的时代时隔170年,久负盛名的雅各布·伯努利在一篇论文中提出了确定悬链线性质(即方程)的问题。实际上,该问题存在多年且一直被人研究。伽利略就曾推测过悬链线是一条抛物线,但问题一直悬而未决。雅各布觉得,应用奇妙的微积分新方法也许可以解决这一问题。
但遗憾的是,面对这个苦恼的难题,他没有丝毫进展。一年后,雅各布的努力还是没有结果,可他却懊恼地看到他的弟弟约翰·伯努利发表了这个问题的正确答案。而自命不凡的约翰,却几乎不可能算是一个谦和的胜利者,因为他后来回忆说:
我哥哥的努力没有成功;而我却幸运得很,因为我发现了全面解开这道难题的技巧(我这样说并非自夸,我为什么要隐瞒真相呢?)……没错,为研究这道题,我整整一晚没有休息……不过第二天早晨,我就满怀欣喜地去见哥哥,他还在苦思这道难题,但毫无进展。他像伽利略一样,始终以为悬链线是一条抛物线。停下!停下!我对他说,不要再折磨自己去证明悬链线是抛物线了,因为这是完全错误的。
可笑的是,约翰成功地解出这道难题,仅仅牺牲了“整整一晚”的休息时间,而雅各布却已经与这道题持续搏斗了整整一年,这实在是一种“奇耻大辱”。
等高悬链线标准方程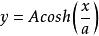
其中,a为常数,是曲线顶点到横坐标轴的距离。1
表达式的证明如右图,设最低点A处受水平向左的拉力H,右悬挂点处表示为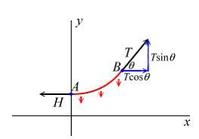 C点,在AC弧线区段任意取一段设为B点,则B受一个斜向上的拉力T,设T和水平方向夹角为θ,AB段绳子的质量为m,显然B点受力平衡,进行受力分析有:
C点,在AC弧线区段任意取一段设为B点,则B受一个斜向上的拉力T,设T和水平方向夹角为θ,AB段绳子的质量为m,显然B点受力平衡,进行受力分析有:
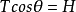
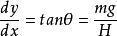
m=σs ,其中s是右段AB绳子的长度,σ是绳子线密度,即单位长度绳子的质量。代入得微分方程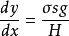 (式1);再利用勾股定理
(式1);再利用勾股定理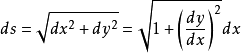 得到式(2):
得到式(2):
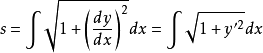
将(2)式代入(1)式得式(3):
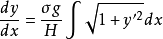
不妨做一次变量替换,令: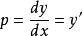 ,得到如下方程:
,得到如下方程:
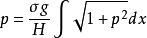
为了将积分符号去掉,对上式两边对x求导:

接下来变量分离并两端进行积分:
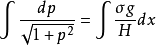
由于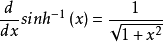 ,所以上面的积分的解为(式4):
,所以上面的积分的解为(式4):
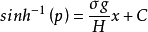
(注意,指数-1表示的是反函数,而不是倒数。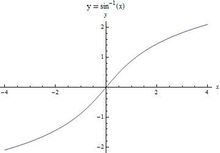 )
)
下面确定C的值。显然,当x=0时,y'=0,即p=0,所以将该初值条件代入我们得到的解,因为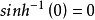 ,解得C=0。下面给出反双曲正弦的图像以加强直观认识。
,解得C=0。下面给出反双曲正弦的图像以加强直观认识。
然后利用反函数的性质,在(4)式的两边取双曲正弦:
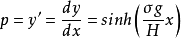
对上式变量分析并积分:
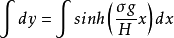
于是得到最终的解:
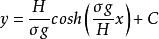
上式中的C一般保留,它会随着坐标系选择的不同而取不同的值。
悬流体方程(1)微分方程为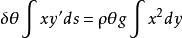 ,方程解为
,方程解为 :
:
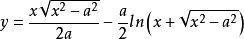
以下是不同a的曲线族。方程原理同悬链线一样。不同的是其表面张力分量必须等于悬挂部分的重力。
垂直方向的流体必须考虑悬流体部分,此部分不是自由流动的流体,其完全受表面张力作用。
如果张力仅仅能够维持自身旋转体重量时,摩擦阻力不考虑。
(2)垂直管道中,或者空气柱内,摩擦阻力与y正比,反重力方向,则微分方程为:
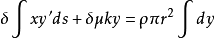
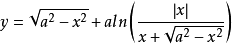
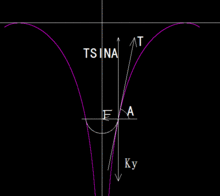
此类如同自然水管龙头的低速流体,但是它需要一个水平方向的张力作用,大小等于ky,第一类与二类均需要。
(2)水平转换张力球,水龙头如果开到很小,会发现,在最底端,水是以一个一个的小球发出,而这个小球就是张力球,水按照一定频率从悬流体中流出,而不是连续的流体,与量子力学基本相通,微分方程如下:
 解出方程为:
解出方程为:
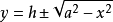 方程是圆球。
方程是圆球。
悬膜壳或者悬流体膜微分方程为: 
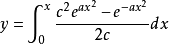
利用积分程序绘图如下:
工程中的应用悬索桥、双曲拱桥、架空电缆、双曲拱坝都用到悬链线的原理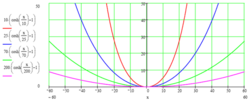 。 在工程中有一种应用,a称作悬链系数。如果我们改变公式的写法,会给工程应用带来很大帮助,公式及图像如下:
。 在工程中有一种应用,a称作悬链系数。如果我们改变公式的写法,会给工程应用带来很大帮助,公式及图像如下:
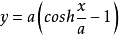
还有以下几个公式,可能也有用:
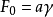
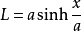
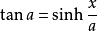
其中L是曲线中某点到0点的链索长度,α是该点的正切角,F0是0点处的水平张力,γ是链索的单位重量。利用上述公式即能计算出任意点的张力。
相关公式双曲正弦的导数: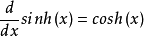
双曲余弦的导数: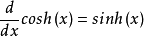 ;
;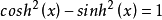
反双曲正弦的导数: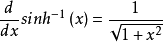
反双曲余弦的导数: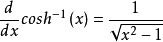




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国