[科普中国]-标准正态分布

定义

标准正态分布又称为u分布，是以0为均数、以1为标准差的正态分布，记为N（0，1）。

标准正态分布曲线下面积分布规律是：在-1.96～+1.96范围内曲线下的面积等于0.9500，在-2.58～+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表（自由度为∞时），借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数均数为0, 尺度参数：标准差为1的正态分布（见下图中绿色曲线）。

特点密度函数关于平均值对称

平均值与它的众数（statistical mode）以及中位数（median）同一数值。

函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。

95.449974%的面积在平均数左右两个标准差的范围内。

99.730020%的面积在平均数左右三个标准差的范围内。

99.993666%的面积在平均数左右四个标准差的范围内。

函数曲线的反曲点（inflection point）为离平均数一个标准差距离的位置。

标准偏差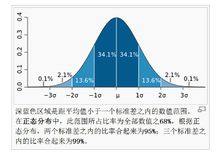

深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比率为全部数值之68%，根据正态分布，两个标准差之内的比率合起来为95%；三个标准差之内的比率合起来为99%。

在实际应用上，常考虑一组数据具有近似于正态分布的概率分布。若其假设正确，则约**68.3%数值分布在距离平均值有1个标准差之内的范围，约95.4%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%**数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”1。