定义
形式幂级数是一个数学中的抽象概念,是从幂级数中抽离出来的代数对象。形式幂级数和从多项式中剥离出来的多项式环类似,不过允许(可数)无穷多项因子相加,但不像幂级数一般要求研究是否收敛和是否有确定的取值。形式幂级数在代数和组合理论中有广泛应用。
设x是一个符号,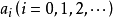 为实数,则
为实数,则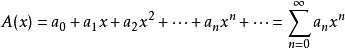 称为以x为未定元的一个形式幂级数。约定:如果在形式幂级数
称为以x为未定元的一个形式幂级数。约定:如果在形式幂级数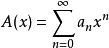 中某个
中某个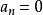 ,则
,则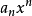 可略去。1
可略去。1
在形式幂级数中,x从来不指定一个数值,且对收敛和发散的问题不感兴趣,感兴趣的是系数序列(a(0),a(1),...,a(n),...),我们研究形式幂级数完全可以归结为讨论这些系数序列,且这些系数序列又可看作含有分量a(0),a(1),...,a(n),...的无穷矢量,系数a(0)称为级数的常数系数。2
形式幂级数的运算我们把形式幂级数看做是收敛的并在其上作代数运算。
已知两个形式幂级数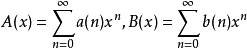 ,则两级数之间可进行如下运算:2
,则两级数之间可进行如下运算:2
相等若对所有的n>0,有a(n)=b(n),则称两形式幂级数相等,有A(x)=B(x)。2
和两形式幂级数的和定义为: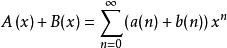 。两形式幂级数的和运算满足交换律和结合律。2
。两形式幂级数的和运算满足交换律和结合律。2
乘积两形式幂级数的乘积定义为: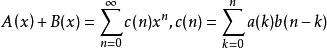 ,称序列{c(n)}为序列{a(n)}与序列{b(n)}的柯西乘积。两形式幂级数的乘积运算对加法满足分配律。2
,称序列{c(n)}为序列{a(n)}与序列{b(n)}的柯西乘积。两形式幂级数的乘积运算对加法满足分配律。2
形式幂级数的逆元逆元的定义设有形式幂级数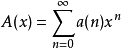 ,若存在形式幂级数
,若存在形式幂级数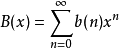 ,使得
,使得 ,则称B(t)是A(t)的一个逆元。1
,则称B(t)是A(t)的一个逆元。1
定理形式幂级数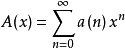 有逆元的充分必要条件是
有逆元的充分必要条件是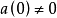 ,且若A(x)有逆元,则逆元必唯一。
,且若A(x)有逆元,则逆元必唯一。
证明:设A(x)有逆元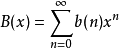 ,因为
,因为 ,所以
,所以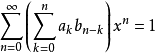 ,从而对任何一个自然数n,有:
,从而对任何一个自然数n,有:
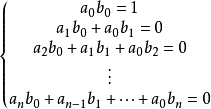 因为
因为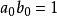 ,所以
,所以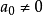 ,把
,把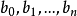 看成未知数,则上述方程组的系数行列式的值
看成未知数,则上述方程组的系数行列式的值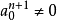 。由克莱姆法则可知,若A(x)有逆元,则
。由克莱姆法则可知,若A(x)有逆元,则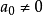 且逆元唯一。
且逆元唯一。
反之,设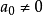 ,令
,令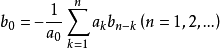 ,则
,则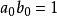 ,且
,且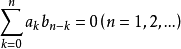 ,于是
,于是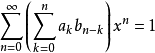 ,令
,令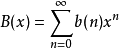 ,则
,则 ,故
,故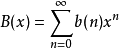 是A(x)的逆元,也就是说当
是A(x)的逆元,也就是说当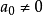 时,
时,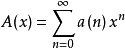 有逆元。1
有逆元。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国