[科普中国]-电子成对能

由于电子之间存在静电排斥，故要将原来以自旋平行的方式处在不同轨道上的两个电子用自旋相反的方式挤到同一个轨道上，就需要克服其间的静电排斥，其所需要的能量称为电子成对能Epair或Ep。

定义当一个轨道中已有一个电子时，若在该轨道填入相反的电子与之成对，而必须克服的电子与电子之间的静电排斥作用能称为电子成对能，记为Epair或Ep。

显然，电子成对能不仅与原子、分子的类型有关，还取决于其轨道的空间分布形状，依赖于库仑积分与交换积分K（θ）。

鉴于Ep>0，故为了使多电子体系的能量降低，对于具有相同能量的轨道而言，电子倾向于以自旋平行的方式占据尽可能多的等价轨道，这就是洪特规则。由此可见，洪特规则并不是一个独立的原理，它是保里不相容原理与能量最低原理在L-S偶合情况下的定量表示。

多电子体系的能级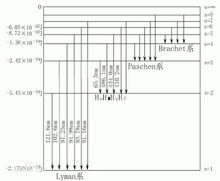由玻尔的理论发展而来的现代量子物理学认为原子核外电子的可能状态是不连续的，因此各状态对应能量也是不连续的。这些能量值就是能级。

对于多电子原子与分子来说，其能级的计算是一个非常困难的工作。由于无法精确求解，故只能借助各种近似方法。例如，在中心场近似下，多电子原子中电子的能级可以粗略地用斯莱特归纳出的一套屏蔽常数σ=σ（n，l）进行估算：。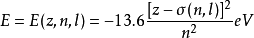

此式说明：多电子原子中电子的能级不仅依赖于原子的种类核电荷z，而且对同一种原子而言还与其主量子数n，角量子数l有关。但是，却与其磁量子数m及自旋量子数ms无关，故具有相同能量的nl亚层含有2l+1个轨道-2（2l+1）个自旋轨道。

因此，当电子处在不同的轨道上时，其能量差将与z、n1、l1及有n2、l2有关。1

电子在原子轨道与分子轨道上的排布无论在原子领域还是在分子领域，保里不相容原理与能量最低原理都是电子排布遵循的两条基本原理，并且在排布时都应考虑电子成对能。

假设所讨论的体系含有5个电子，能量最低的轨道有a、b、c、d、e5个，其能量为Ea、Eb、Ec、Ed、Ee。

若其最大的能量差EΔmax=Ee-Ea小于电子成对能Ep，则根据能量最低原理与保里不相容原理电子将以自旋平行的方式分别占据此5个轨道，如图1所示。自由金属离子Fe3+的电子在3d轨道上的排布情况就是这样。在弱的配位场中的情况也与此类似，从而形成具有很强磁性的高自旋配合物[FeF6]3-。

如果Ep