[科普中国]-等轴双曲线

实轴和虚轴相等的双曲线叫作等轴双曲线(直角双曲线)1。

等轴双曲线是指一种特殊的双曲线，特点是渐近线互相垂直，半实轴长与半虚轴长相等，两条渐近线y=±x互相垂直2。

主要性质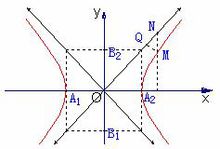

等轴双曲线的主要性质有：

（1）半实轴长=半虚轴长（一般而言是a=b，但有些地区教材版本不同，不一定用的是a,b这两个字母）；

（2）其标准方程为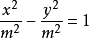，其中m≠0；

（3）离心率e=√2；

（4）渐近线：两条渐近线 y=±x 互相垂直；

（5）等轴双曲线上任意一点到中心的距离是它到两个焦点的距离的比例中项；

（6）等轴双曲线上任意一点P处的切线夹在两条渐近线之间的线段，必被P所平分；

（7）等轴双曲线上任意一点处的切线与两条渐近线围成三角形的面积恒为常数a^2；

（8）等轴双曲线x^2-y^2=C绕其中心以逆时针方向旋转45°后，可以得到XY=a^2/2，其中C≠0。

（9）反比例函数y=k/x的图像一定是等轴双曲线。1

相关命题1.设A是等轴双曲线上一点，A处的法线分别交双曲线的实轴m和虚轴n于B、C，那么，AB=AC2。

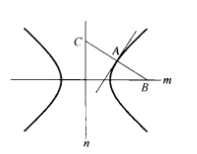
2.设等轴双曲线的中心为M，实、虚轴分别为m、n，过双曲线上一点A作切线，且交n于B，设AM与m所成的角为α，AB与n所成的角为β，那么，α=β2。

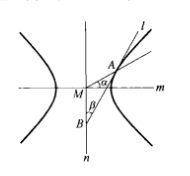
3.过等轴双曲线的焦点F作两条互相垂直的直线，且分别交双曲线于A、B和C、D，那么，AB=CD2。

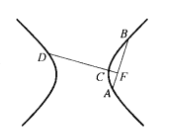
4.以等轴双曲线的弦AB为直径作圆，且交双曲线于C，过C作AB的垂线CS，那么，CS是双曲线的切线2。

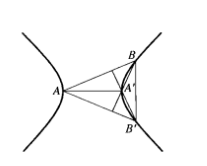
5.设等轴双曲线的实轴为AA’，弦BB’与AA’垂直，那么，AB⊥A’B’，A’B上AB’2。

本词条内容贡献者为:

尚轶伦 - 副教授 - 同济大学数学科学学院