[科普中国]-自相关函数

定义

在统计学上，自相关被定义为，两个随机过程中不同时刻的数值之间的皮尔森相关(Pearson correlation).

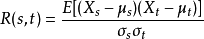
如果X为广义平稳过程，则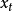的期望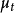以及标准差不随时间t变化，则自相关函数可以表示为时间延迟的函数，如下

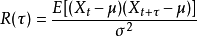
信号处理

，

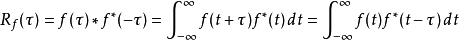其中“*”是卷积算符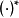，为取共轭。

同一时间函数在瞬时t和t+a的两个值相乘积的平均值作为延迟时间t的函数，它是信号与延迟后信号之间相似性的度量。延迟时间为零时，则成为信号的均方值，此时它的值最大。2

简而言之，自相关函数是表达信号和它的多径信号的相似程度。一个信号经过类似于反射、折射等其它情况的延时后的副本信号与原信号的相似程度。

性质以下以一维自相关函数为例说明其性质，多维的情况可方便地从一维情况推广得到。

对称性：从定义显然可以看出R(i) = R(−i)。连续型自相关函数为偶函数。

当f为实函数时，有：

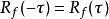
当f是复函数时，该自相关函数是厄米函数，满足：

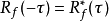
其中星号表示共轭。

连续型实自相关函数的峰值在原点取得，即对于任何延时 τ，均有 |R_f(\tau)| \leq R_f(0)。该结论可直接有柯西-施瓦兹不等式得到。离散型自相关函数亦有此结论。2

周期函数的自相关函数是具有与原函数相同周期的函数。

两个相互无关的函数（即对于所有 τ，两函数的互相关均为0）之和的自相关函数等于各自自相关函数之和。

由于自相关函数是一种特殊的互相关函数，所以它具有后者的所有性质。

连续时间白噪声信号的自相关函数是一个δ函数，在除 τ = 0 之外的所有点均为0。

维纳-辛钦定理（Wiener–Khinchin theorem）表明，自相关函数和功率谱密度函数是一对傅里叶变换对：

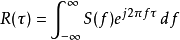
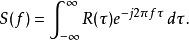
实值、对称的自相关函数具有实对称的变换函数，因此此时维纳-辛钦定理中的复指数项可以写成如下的余弦形式：

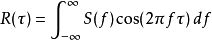
举例白噪声的自相关函数为δ函数：

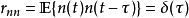
具有罗伦兹功率谱的色噪声的自相关函数为:

=

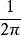
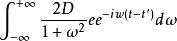
应用信号处理中，自相关可以提供关于重复事件的信息，例如音乐节拍（例如，确定节奏）或脉冲星的频率（虽然它不能告诉我们节拍的位置）。另外，它也可以用来估计乐音的音高。