[科普中国]-角平分线

定义

1.从一个角的顶点引出一条射线（线在角内），把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线(bisector of angle)。

2.角平分线是在角的型内及形上，到角两边距离相等的点的轨迹。

性质1.角平分线分得的两个角相等，都等于该角的一半。（定义）

2·角平分线上的点到角的两边的距离相等。

判定角的内部到角的两边距离相等的点，都在这个角的平分线上。1

因此根据直线公理。

证明：如图，已知PD⊥OA于D，PE⊥OB于E，且PD=PE，求证：OC平分∠AOB

证明：在Rt△OPD和Rt△OPE中：

OP=OP，PD=PE

∴Rt△OPD≌Rt△OPE（HL）

∴∠1=∠2

∴ OC平分∠AOB

角平分线定义在三角形中的定义。

三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）。 由定义可知，三角形的角平分线是一条线段。 由于三角形有三个内角，所以三角形有三条角平分线。三角形的角平分线交点一定在三角形内部。

角平分线性质在三角形中的性质。

1.三角形的三条角平分线交于一点，且到各边的距离相等.这个点称为内心 (即以此点为圆心可以在三角形内部画一个内切圆)。2

2.三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例。

如图，若AD是△ABC的角平分线，则 BD/DC=AB/AC 。

证明：作CE∥AD交BA延长线于E。

∵CE∥AD

∴△BDA∽△BCE

∴BA/BE=BD/BC

∴ BA/AE=BD/DC

∵CE∥AD

∴∠BAD=∠E,∠DAC=∠ACE

∵AD平分∠BAC

∴∠BAD=∠CAD

∴ ∠BAD=∠CAD=∠ACE=∠E

即∠ACE=∠E

∴ AE=AC

又∵BA/AE=BD/DC

∴BA/AC=BD/DC

以上均为初中阶段知识点及证法，详见“角平分线定理”“三角形角平分线”。

作法

方法一：1.以点O为圆心，以任意长为半径画弧，两弧交角AOB两边 于点M，N。

2.分别以点M，N为圆心，以大于1/2MN的长度为半径画弧， 两弧交于点P。

3.作射线OP。

射线OP即为所求。

证明：连接PM,PN

在△POM和△PON中

∵OM=ON,PM=PN,PO=PO

∴△POM≌△PON(SSS)

∴∠POM=∠PON，即射线OP为角AOB的角平分线

当然，角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。

方法二：1.在两边OA、OB上分别截取OM、OC和ON、OD，使OM=ON，OC=OD；

2.连接CN与DM，相交于P；

3.作射线OP。

射线OP即为所求。

内心任意三角形ABC中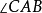，、、角平分线交于一点I，则我们称此点I为三角形ABC的内心。

三角形的内心恒在图形内部，且到三角形之三边距离等长。