[科普中国]-高斯积分

高斯积分计算公式：

计算公式：1

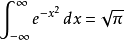
高斯函数的积分任何高斯函数的积分均可简化为含高斯积分的项。2

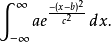
常数a可以被提出积分。使用y=x-b来取代x-b获得

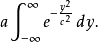
使用z=y/c取得

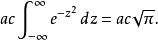
高斯积分求解高斯积分在概率论和连续傅里叶变换等的统一化等计算中有广泛的应用。在误差函数的定义中它也出现。虽然误差函数没有初等函数，但是高斯积分可以通过微积分学的手段解析求解。

（Gaussian quadrature）

首先我们说明一下这里使用积分的符号：

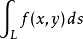表示f(x,y)在曲线L上的第一型曲线积分。

首先看第一型曲线积分形式的高斯积分：

设L是一条曲线，r是这曲线一点到L外一点A(e,m)的连接向量，n是曲线这一点的法向量，(r,n)表示r与n向量的夹角，则积分为：

d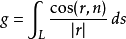

高斯积分的几何意义就是：

g是从点A所能看到曲线L的角的度量。

设(x,n)是x轴正方向与n的夹角，(x,r)是x轴正方向与r的夹角，则

(r,n) = (x,n) - (x,r)

所以：

cos(r,n) = cos(x,n)cos(x,r)+sin(x,n)sin(x,r)

=((x-e)cos(x,n)/|r| + (y-m)sin(x,n)/|r|

代入高斯积分：

g = ∫[L] ((y-m)sin(x,n)/(|r|2) + (x-e)cos(x,n)/(|r|2)) ds

化成第二型曲线积分：

g = ±∫[L] ((y-m)/(|r|2) dx - (x-e)/(|r|2) dy)

±表示法线n的两个方向。

此方程满足积分路径无关的条件，假如L是一条闭曲线，A在L外部，那么g=0，如果A在内部，根据挖奇点法，积分结果为2π。3

人物简介——高斯德国布隆斯威克人。德国的数学家、物理学家和天文学家。高斯幼年时就显示出非凡的数学才能，得到Carl Wil-helm Ferdinand大公的赏识。在大公的支持下，1795—1798年在哥廷根(Gottingen)大学学习，1799年因证明代数学的基本定理而获得哈勒(Halle)大学的博士学位。从1807年到1855年逝世，一直担任哥廷根天文台台长兼大学教授。1796年用直尺圆规作出了正十七边形一自欧几里得以来两千年间几何作图的一个难题。接着又证明了数论中的欧勒猜想—二次互反律。 据说从此后他决心放弃古典文学而献身于数学。1801年用自己的行星轨道计称法和最小二乘法算出了意大利天文学家皮亚齐 (1746—1826) 发现的谷神星轨道; 谷神星的轨道计算使他一举名震世界。同年，出版经典著作《算术研究》，任职期间，高斯致力于数论、代数、几何、分析、复变函数、统计数学等多方面的研究、取得了一系列的成果。高斯定理、高斯公式、高斯函数等以他命名的多种发现至今仍在许多数学、科学部门中闪烁着光辉。高斯还涉足了大地测量工作。 为了进行长距离测量，发明了“目光反射器”，并在理论上创造了“大地问题解法”，导致他开创了曲面微分几何的理论。并由他的学生黎曼发展为黎曼几何。与德国的物理学家韦伯(wilhelm Eduavd Weber，1804—1891)一道建立了电磁学中的高斯单位制; 1833年还和韦伯一起发明了电磁电极。高斯的治学态度十分严谨。他的格言是 “瑰丽的大厦建成后，应拆除杂乱无章的脚手架。” 因此他发表的每篇著作都是经过仔细推敲、无懈可击的精品。因此，发表的论文比研究工作要少得多，但研究项目可在日记和书信中见到。全集包括日记、书信共计12卷。他是19世纪前半世纪最伟大的数学家。4