[科普中国]-概率密度

定义

对于随机变量X的分布函数F（x），如果存在非负可积函数f(x)，使得对任意实数x,有

则X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度。

单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。可以把概率密度看成是纵坐标，区间看成是横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率，所有面积的和为1。所以单独分析一个点的概率密度是没有任何意义的，它必须要有区间作为参考和对比。

性质非负性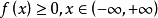

规范性这两条基本性质可以用来判断一个函数是否为某一连续型随机变量的概率密度函数。1

物理概念电子运动的状态有波函数Ψ来描述，|Ψ|²表示电子在核外空间某处单位体积内出现的概率，即概率密度。处于不同运动状态的电子，它们的|Ψ|各不相同，|Ψ|²当然也不同。密度大则事件发生的分布情况多，反之亦然。若用黑点的疏密程度来表示各个电子概率密度的大小，则|Ψ|²大的地方黑点较密，其概率密度大，反之亦然。在原子和外分布的小黑点，好像一团带负电的云，把原子核包围起来，人们称它为电子云。

1926年，奥地利物理学家薛定谔运用偏微分方程，建立了描述微观粒子运动的波动方程，即薛定谔方程。由薛定谔方程式的可知，对于一个质量为m，在势能为V的势场中运动的微粒来说，有一个与这个微粒运动相联系的波函数ψ，这个波函数就是薛定谔方程的一个合理的解，每一个解都与相应的常数E对应，就是微粒在这一运动状态的能量（或能级）。|Ψ|²表示原子核外空间某点P(x,y,z)处电子出现的概率密度，即在该点处单位体积中电子出现的概率。用来表示概率密度的几何图形俗称电子云，电子云并非众多电子弥散在核外空间，而是电子在核外空间各处出现的概率密度的形象表现。