[科普中国]-吸收律

简述

设有某个集合闭合在两个二元运算下。如果这些运算是交换律、结合律的，并满足吸收律，结果的抽象代数就是格，在这种情况下这两个运算有时叫做交和并。因为交换律和结合律经常是其他代数结构的性质，吸收律是格的定义性质。由于布尔代数和 Heyting代数是格，它们也服从吸收律。

因为经典逻辑是布尔代数的模型，直觉逻辑是 Heyting代数的模型，吸收律对分别指示逻辑或和逻辑与的运算。

定义吸收律对相干逻辑、线性逻辑和亚结构逻辑不成立。在亚结构逻辑情况下，在恒等式的定义对的自由变量之间没有一一对应。

吸收律的证明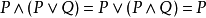

(P ∨ 0) ∧ (P ∨ Q) = P ∨ (0 ∧ Q) = P ∨ 0 = P

(P ∧ 1) ∨ (P ∧ Q) = P ∧ (1 ∨ Q) = P ∧ 1 = P

这里的 = 号要理解为公式上的逻辑等价。1

吸收律对相干逻辑、线性逻辑和亚结构逻辑不成立。在亚结构逻辑情况下，在恒等式的定义对的自由变量之间没有一一对应。

相关理论格理论、布尔代数。