[科普中国]-哈斯图

简介

哈斯图得名于Helmut Hasse（1898年–1979年）；依据Birkhoff (1948)，这么叫是因为Hasse有效的利用了它们。但是Hasse不是第一个使用它们的人，它们早就出现在如Vogt (1895)中。尽管哈斯图被设计为手工绘制偏序集合的技术，最近已经使用图绘制技术自动来生成它们了。1

术语“哈斯图”还可以称呼作为抽象有向无环图的传递简约，独立于这个图的任何绘制形式。但是这里不采用这种用法。

图中的每个结点表示集合A中的一个元素，结点的位置按它们在偏序中的次序从底向上排列。即对任意a，b属于A，若a≤b且a≠b,则a排在b的下边。如果a≤b且a≠b，且不存在c∈A满足a≤c且c≤b，则在a和b之间连一条线。这样画出的图叫哈斯图，又称偏序集合图。

作图法（1）以“圆圈”表示元素；

（2）若x≤y,则y画在x的上层；

（3）若y覆盖x,则连线；

（4）不可比的元素可画在同一层。

例题：画出下列各关系的哈斯图

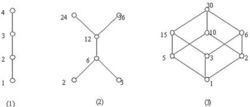
1）P={1,2,3,4},的哈斯图。

2）A={2,3,6,12,24,36},的哈斯图。

3）A={1,2,3,5,6,10,15,30},的哈斯图。

解如图：哈斯图L-12

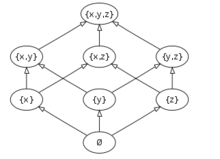
例子{ x, y, z }的幂集按包含偏序排序，有哈斯图:

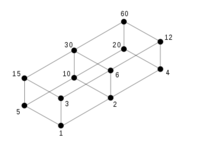
所有60的除数的集合A = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 }，按整除性排序，有哈斯图:

集合{ 1, 2, 3, 4 }的所有15个划分，按精细度（就是更细划分小于更粗划分）排序，有哈斯图:

好的哈斯图尽管哈斯图是简单的处理有限偏序集的直观工具，绘制出好的哈斯图是非常困难的。原因是对于给定偏序集有任意多种可能的绘图方式。简单的技术就是开始于这个次序的最小元并逐步增加上更大的元素，这经常产生非常窘迫的结果：很容易丢失了这个次序的对称性和内部结构。

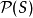下面的例子展示这个问题。考虑集合S = {a, b, c, d}的幂集，就是说S的所有自己的集合，按照子集包含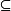来排序。下面是这个偏序的三个不同哈斯图:

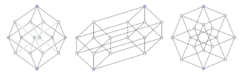
通过使得在这个幂集中每个集合的y坐标成比例于集合的势，最左图示展示了这个幂集是等级偏序集。中间图示有相同的等级结构，但使得某些边比其他边长，它把这个幂集的结构强调为两个三维立方体的联合：在两个立方体中下面的那个中的顶点表示不包含S的某个特定元素比如d的集合，而上面立方体的顶点表示包含d的集合。最右图示展示了这个结构的某种内部对称性。