[科普中国]-全关系

定义

在数学中，集合X上的一个二元关系R是全关系（total relation），若其满足：“对所有属于X的a和b，a关系到b或b关系到a。”

可用符号表示为：

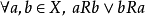
上述性质一般也称为完全性（totality）。

实例实数集上的“小于等于”是一个全关系，而“严格小于”则不是。

整除不是一个全关系，因为整数6和8都不能整除对方。

例如，“小于或等于”是与实数集合之间的总关系，因为两个数字是第一个小于或等于第二个数，或者第二个数小于或等于第一个。 另一方面，“少于”不是一个完全关系，因为人可以选两个相等的数字，而不是第一个小于第二个，也不是第二个小于第一个。 （但请注意，“少于”是一种弱势，导致总体秩序，即“小于或等于”，严格秩序与弱指令之间的关系在部分有序集上讨论。）1

关系“是”的一个子集“也不是全部的，因为例如集合{1,2}和{3,4}都不是另一个的子集。

特性完全性蕴涵自反性。

满足传递性的全关系是弱序关系。满足完全性的偏序关系是全序关系。