[科普中国]-功效函数

引入

在进行假设检时，我们要确立原假设和备择假设，为了选择哪种假设，我们规定了拒绝域。如果样本落在拒绝域内，我们拒绝原假设，接受备择假设，否则接受原假设。这样我们在应用某种检验做判断时，可能会犯如下两种错误：原假设是对的，我们却拒绝了原假设，这称为第一类错误；相反，原假设是错的，我们却接受了原假设，这称为第二类错误。1在检验中我们希望犯两类错误的概率都尽可能地小，但实际上我们做不到这一点，为了说明原因，我们需要引进功效函数这一概念。2

定义设某检验问题的拒绝域为W，则样本观测值X落在拒绝域W内的概率称为该检验的功效函数，记为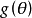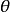，为原假设和备择假设中的参数。3

性质当原假设成立时，犯第一类错误的概率就等于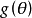。当备择假设成立时，犯第二类错误的概率就等于。

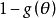下面我们通过一个例子来说明我们无法使一个检验犯第一类、第二类错误的概率同时减少。

某厂生产的合金强度服从正态分布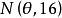，其中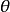的设计值为不低于110。为保证质量，该厂每天都要对生产情况做例行检查，以判断生产是否正常进行，即该合金的平均强度不低于110。某天从生产的产品中随机抽取25块合金，测得其强度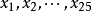值为，均值为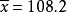，问当日生产是否正常。

对于本例，其拒绝域为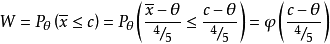

注意到这个功效函数是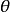的减函数，如右图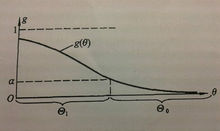利用这个功效函数易得犯两类错误的概率分别为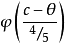（原假设成立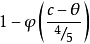），（备择假设成立）。

由此可以得出犯两类错误的概率之间的关系：

1、当第一类错误的概率减少时，c随之减小，而c的减小必导致犯第二类错误的概率增大。

2、当第二类错误的概率减少时，c随之增大，而c的增大必导致犯第一类错误的概率增大。

这一现象说明：两类错误的一个减小必导致另一个的增大。