[科普中国]-分段线性化法

简介

把非线性特性曲线分成若干个区段，在每个区段中用直线段近似地代替特性曲线，这种处理方式称为分段线性化。在分段线性化处理后，所研究的非线性系统在每一个区段上被近似等效为线性系统，就可采用线性系统的理论和方法来进行分析。将各个区段的分析结果，如过渡过程曲线或相轨迹(见相平面法)，按时间的顺序加以衔接，就是所研究非线性系统按分段线性化法分析得到的结果。

举例说明分段线性化法的原理和分析步骤的一个例子是简单非线性电路系统。电路由电阻R和铁芯线圈L串接组成，通过开关接入一个直流电源。根据电路原理可知，描述这个电路在开关闭合后电流增长过程的运动方程是一个非线性微分方程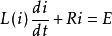： ，式中i表示电流,R表示电阻,L(i)表示铁芯线圈的非线性电感,为i的函数。非线性电感可表示为 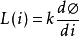，其中k为常数,磁通φ和电流i之间的关系具有非线性特性。

电路的初始电流为i(0)=0，而在到达稳态时电路的稳态电流为I(∞)=E/R。在采用分段线性化法来分析时,先在电流值的有效区间[0,i(∞)]内，将非线性特性分成N个区段，且在每个区段内用直线近似代替曲线。

在定出每个直线段和水平线的交角θ0₀、θ₁、θ₂后，可知相应于每个区段的等效线性电感值为L₀=K₀tgθ₀、L₁=K₁tgθ₁和L₂=K₂tgθ₂,其中K₀、K₁、K₂为不同的常数。因此，在每一个区段,电路的运动方程都是线性的：

区段Ⅰ：;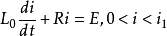

区段Ⅱ：;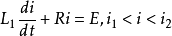

区段Ⅲ：。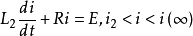

这些线性微分方程可用线性分析方法求解，其分析结果为

区段Ⅰ：;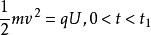

区段Ⅱ：;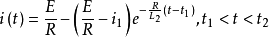

区段Ⅲ：。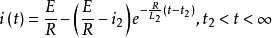

式中时间t1和t2的值可由区段Ⅰ和Ⅱ的电流表达式定出：。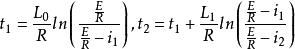

这一非线性电路按分段线性化法分析的解就是三个区段内的分析结果在时刻t1和t2上衔接所得到的运动过程。

分段线性化法的分析精度和计算复杂性取决于系统非线性程度的高低。对于具有折线形状的非线性特性，如继电型非线性和死区非线性（见描述函数法），分段线性化法不会引入分析误差，且计算上也不会增加复杂性。对于非线性程度较低的系统，分段线性化法具有比较好的分析结果。对于非线性程度高的系统，原则上分段线性化法仍可适用，但计算复杂性增加，而分析准确度则取决于线性化的区段数的多少。1