[科普中国]-伪素数

基本信息年表

1903年，马洛（Malo）证明：若n为伪素数，则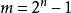 也是一个伪素数，从而肯定了伪素数的个数是无穷的。

1950年，发现第一个偶伪素数161038=2*73*1103。

1951年，皮格（Beeger）证明了存在无限多个偶伪素数。

例子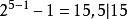 。 。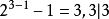但很多都是素数，如3，5，7，29，31……

1819年数学家萨鲁斯找到了反例： ，而341=11*31是合数，341就成了第一个伪素数。以后又发现了许多伪素数：561 645 1105 1387 1729……

其他信息起源能整除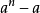 的合数n，a≥2，（a，n）=1，被称为以a为底的伪素数，简记为a-伪素数。

伪素数起源于17世纪法国数学家费马的某些研究。他于17世纪30年代末曾写信给法国数学家梅森，提到这样一个命题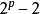： 能被素数p整除。后来，在他1640年10月18日给德贝西的信中说，他进一步证明了这样一个定理：

如果p是一个素数，且a不能被p整除，则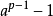 能被P整除（等价的说法是 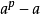能被素数p整除）。

后人称这个定理为费马小定理，以和费马大定理相区别。费马小定理奠定了现代数论中素数判定的基础。

按费马小定理，如果一个奇数n不能整除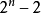 ，则n必为合数（这是费马小定理的一个逆否命题）。但是，如果奇数n>1能整除 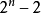， n就一定是素数吗？就是说，费马小定理的逆命题是否成立？对于11，只要（a，n）=1时，n能整除 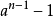，则n被称为卡迈克尔数。这种数是由美国数学家R．D．卡迈克尔于1912年提出来的。最小的卡迈克尔数为561，这种数在自然数中更少了，在10亿之内，只有646个。一个问题就是：卡迈克尔数是否有无穷多？

伪素数谜享有"业余数学之王"称号的费马曾经证明:若p为素数,则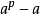 是p的倍数,进一步如果p与a互素,则显然 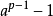是p的倍数,用同余式来表达就是：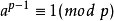

这个表达式无疑是数论大厦的一块基石。对如此美妙的定理如果毫不动心，那他一定是只剩下一口气的行尸走肉。推导这个公式用同余式最方便，由于与素数p互素的数有p-1个，它们是：

1,2,3,...p-1

显然有: a*2a*3a...a(p-1)=1*2*3...(p-1)（ mod p）

即: [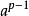 ]*(p-1)!=(p-1)! （mod p）

因为从1到p-1之间的所有整数都于p互质，所以可以两边同除以(p-1)!得到：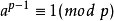

再对a应用数学归纳法即可证明之。2

但是它的逆定理是不成立的，即当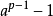 能被p整除时,p不一定是素数，在1819年，法国数学家莎路斯首先发现，虽然341能够整除2340-1，但是341=11*31为一个合数。后来有一位德国数学家一般性地证明了，只要找到两个奇素数p,q，使得它们的积能同时整除 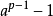与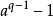 ，那么就可得到pq整除 。

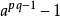伪素数有无穷多个，第一个证明这一点的是数学家迈罗在1903年给出的。如果n是伪素数，则2n-1也是伪素数，所以伪素数有无穷多个。除了上述的341之外，人们陆续发现了561,645,1105,1387,1729,1905等等。数学家普列特在1938年做出了1亿以内的伪素数表。因此伪素数又叫做普列特数。

除了奇伪素数以外,竟然还有偶伪素数存在,美国著名数学家D.H.莱默在1950年找到了第一个偶伪素数：161038，后来荷兰数学家毕格尔又发现了3个偶伪素数：215326,2568226和143742226，并且从理论上证明了存在无穷多个偶伪素数。

伪素数是针对底数为2的情形提出的.而对于一般的底数a，则提出了a-伪素数的概念。例如91能整除390-1，所以把91称为3-伪素数。1904年，意大利数学家奇波拉给出了一种构造a-伪素数的方法：

对于已知的整数 a>=2，取任意奇素数 p，使得 p不能整除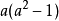 ，则 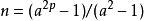必是a-伪素数。比如取 a=2，选 p=5，显然 5不能整除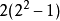，所以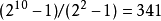 是伪素数。1

对于已知的整数 a>=2，由于有无穷多个奇素数不能整除a(a^2-1)，所以a-伪素数有无穷多个。

利用伪素数表,数学家D.H.莱默建议按照如下程序来判别一个奇数是否是素数：如果p不能整除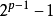，则p必然为合数；如果p能整除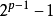，且p在伪素数表中，则p为合数，否则p为素数。显然这是基于费马小定理的检验法，我想如果再结合筛法,就会完全剔除这些伪素数。

毕竟伪素数比较稀少，在前10亿个自然数中共有50847534个素数，而伪素数只有5597个，即大约只占万分之一。而同时能以2,3为底的伪素数只有1272个，即大约5万分之一。那么是否存在这样的数p，它能够整除所有的以2,3,4,...为底的费马表达式，那么p一定是素数了吧?遗憾的是，竟然存在这样的伪素数，它能够整除以任何整数a为底(即使是负整数)的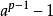,561就是最小的一个例子：

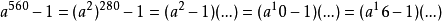
由于561=3*11*17，而由费马小定理，3,11,17都能够整除上式，所以561也能够整除上式。这种极端的伪素数叫做绝对伪素数，又由于是首先由美国数学家卡迈克尔在1912年发现的，所以又叫做卡迈克尔数，为了判别什么样的整数是卡迈克尔数，他发现了一个准则：

如果整数n满足如下条件

(1) n没有平方因子，即n没有相同的素因子；

(2) n是奇数且至少有3个不同的素数因子；

(3) 对于n的每一个素数因子p,p-1能够整除n-1；

则 n 必为卡迈克尔数。反之，如果 n是卡迈克尔数，则 n必满足上述3个条件。

1939年,数学家切尼克给出了一种构造卡迈克尔数的方法：

设m为自然数，且使得(6m+1),(12m+1),(18m+1)都是素数，则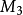 (m)=(6m+1)(12m+1)(18m+1)是具有3个素因子的卡迈克尔数。例如取m=1，则有 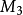(1)=7*13*19=1729是卡迈克尔数。类似地，自然数m是使得 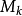(m)=(6m+1)(12m+1)(9*2m+1)...(9*2k-2m+1) (k>=4)中k个因子都是素数，则 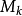(m)是含有k个素因子的卡迈克尔数。1985年，杜伯纳得到了下面一些巨大的卡迈克尔数: m=5*7*11*13*...*397*882603*10185 时的含有3个素因子的卡迈克尔数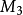(m)是一个1057位数，这是目前知道的最大的卡迈克尔数。其他的还有：

m=323323*655899*1040/6 时的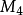(m)是个207位数的卡迈克尔数。

m=323323*426135*1016/6 时的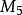(m)是个139位数的卡迈克尔数。

m=323323*239556*107/6 时的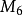(m)是个112位数的卡迈克尔数。

m=323323*160*8033 时的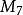(m)是个93位数的卡迈克尔数。

1978年，约里纳戈发现了8个卡迈克尔数，它们都具有13个素数因子。这是目前所知道的含有素数因子最多的一组卡迈克尔数。下表是目前所知道的小于x的以2为底的伪素数个数P(x)与卡迈克尔数的个数C(x)的分布情况。

x P(x) C(x)

不超过100000的16个卡迈克尔数如下：

561,1105,1729,2465,2821,6601,8911,10585,15841,29341,41041,46657,52633,62745,63973,75361

留给人们的未解之谜是;

(1) 同时以a,b为底的伪素数是否有无穷多个?

(2) 卡迈克尔数是否有无穷多个?

爱多士猜想有无限个卡迈克尔数，1994年 William Alford 、 Andrew Granville 及 Carl Pomerance 证明了这个命题。

强伪素数令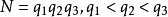 是三因子的Carmicheal数，定义C3，1-及C3，2-数，它们分别指 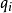=5 mod 8,i=1,2,3及 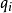≡5 mod 8,i=1,2, 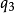≡9 mod 16时的情况，它们有着较高的成为强伪素数的概率。本文首先给出成为这些数的充分必要条件然后给出算法，最后经过上机计算得到1024以内的有58个对于前5个素数基的C3,1-强伪素数，其中有一个是对于前8个素数基的强伪素数；以及27个对前4个素数基的C3,2-强伪素数，只有一个是对于前4个基的强伪素数。1

素数与伪素数通项公式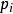 为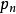 集合内元素，所有以 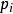为因子的伪素数的n的取值公式为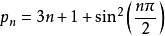

伪素数变量的充分与必要条件：1.n为奇数时：n(x,y)=3xy+x+2y,或者n(x,y)=3xy+2x+y，计算时必须满足n(x,y)为奇数。

2.n为偶数时：n(x,y)=3xy+x+y,或者n(x,y)=3xy+2x+2y+1，计算时必须满足n(x,y)为偶数。

满足以上条件的n,其对应的数必为伪素数。3

素数变量的充分与必要条件：1.n为奇数时：n(x,y)≠3xy+x+2y,或者n(x,y)≠3xy+2x+y，计算时必须满足n(x,y)为奇数。

2.n为偶数时：n(x,y)≠3xy+x+y,或者n(x,y)≠3xy+2x+2y+1，计算时必须满足n(x,y)为偶数。

满足以上条件的n,其对应的数必为素数。2