定义
定义1(矩量母函数)设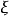 为随机变量,若存在某正实数
为随机变量,若存在某正实数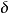 ,使得对于区间
,使得对于区间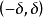 中任一实数t,数学期望
中任一实数t,数学期望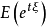 均存在,则称
均存在,则称
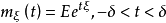 为随机变量
为随机变量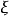 或其分布的矩量母函数(moment generating function),简记为mgf.1
或其分布的矩量母函数(moment generating function),简记为mgf.1
另外,称矩量母函数的对数为累积量生成函数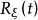 。
。
与特征函数的联系定义2(特征函数)设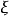 为随机变量,称复随机变量
为随机变量,称复随机变量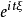 的数学期望
的数学期望
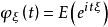 为
为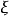 的特征函数,其中t为实数。
的特征函数,其中t为实数。
特征函数具有以下性质:
(1)如果两个随机变量具有相同的特征函数,那么它们具有相同的概率分布; 反之, 如果两个随机变量具有相同的概率分布, 它们的特征函数也相同(显然)。
(2)独立随机变量和的特征函数等于每个随机变量特征函数的乘积。
综合定义1和定义2,可得随机变量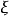 的特征函数与其mgf之间存在如下关系:
的特征函数与其mgf之间存在如下关系:
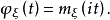
对比特征函数的性质,随机变量的mgf也具有如下常用性质:
(1)如果两个随机变量具有相同的mgf,那么它们具有相同的概率分布; 反之, 如果两个随机变量具有相同的概率分布, 它们的mgf也相同。(即在mgf存在的情况下,随机变量的mgf与其概率分布相互唯一确定。)
(2)独立随机变量和的mgf等于每个随机变量mgf的乘积。
性质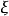 以连续随机变量为例,离散型随机变量可做相同变换。
以连续随机变量为例,离散型随机变量可做相同变换。
(1)由泰勒级数
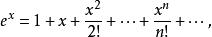 有
有
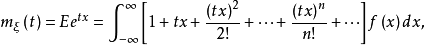 即
即
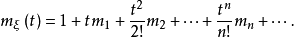 其中,
其中,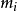 是随机变量
是随机变量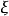 的i阶中心矩。
的i阶中心矩。
(2)mξ(-t)是双侧拉普拉斯变换(Laplace Transform)。
(3)不管概率分布是不是连续,矩量母函数都可以用黎曼-斯蒂尔切斯积分给出:
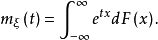 其中,F(x)是累积分布函数(Cumulative Distribution Function, 简称CDF)。2
其中,F(x)是累积分布函数(Cumulative Distribution Function, 简称CDF)。2
应用常见分布的mgf对于随机变量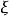 ,有如下结论:1
,有如下结论:1
(1)若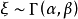 ,则
,则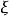 的mgf为
的mgf为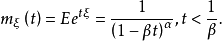
(2)若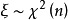 ,则
,则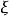 的mgf为
的mgf为
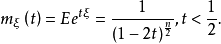
(3)若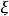 服从参数为
服从参数为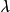 的指数分布,则
的指数分布,则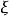 的mgf为
的mgf为
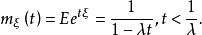
求随机变量的矩设随机变量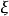 的矩量母函数存在,则
的矩量母函数存在,则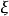 的各阶矩存在且可由矩量母函数表示。具体地,
的各阶矩存在且可由矩量母函数表示。具体地,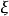 的k阶矩为矩量母函数在0点的k阶导数值,即对任意正整数k,有
的k阶矩为矩量母函数在0点的k阶导数值,即对任意正整数k,有
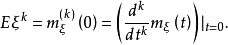 特别地,有
特别地,有
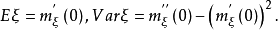
证明:由泰勒级数
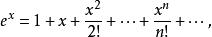 有
有
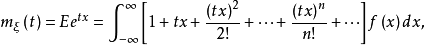 即
即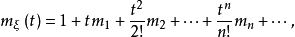 其中,
其中,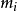 是随机变量
是随机变量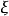 的i阶中心矩。上式左右两边同时对t求n阶导,得到
的i阶中心矩。上式左右两边同时对t求n阶导,得到
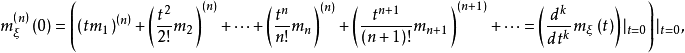 故
故
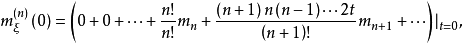 即
即
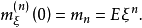 证毕。
证毕。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国