指数积分的定义
n阶指数积分(Exponential Integral)为
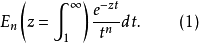
对正整数n≥1,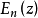 与
与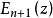 之间的递推关系为
之间的递推关系为
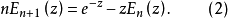
当自变量为正实数且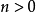 时,函数
时,函数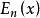 满足如下不等式1
满足如下不等式1
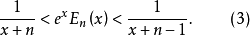
一阶指数积分一阶指数积分(虚数自变量)是自变量取纯虚数时的积分(即式(1)中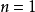 )1
)1
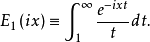 该式也可以表示为如下等效形式
该式也可以表示为如下等效形式
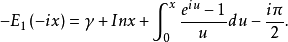 式中:
式中: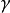 为欧拉一马歇罗尼常数(Euler-Mascheroni constant):
为欧拉一马歇罗尼常数(Euler-Mascheroni constant):
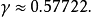
三阶指数积分三阶指数积分(实数自变量)是自变量为正实数的指数积分(即式(1)中n=3)为
 这一函数可用来计算无限片状分布声源的辐射噪声场。对所有
这一函数可用来计算无限片状分布声源的辐射噪声场。对所有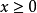 都有效的一个近似式(基于式(3))为
都有效的一个近似式(基于式(3))为
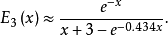 对于在区间
对于在区间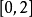 上取值的x,此近似式的最大相对误差为2%。1
上取值的x,此近似式的最大相对误差为2%。1
正弦积分函数与余弦积分函数正弦积分函数(Sine Integral Function)与余弦积分函数(Cosine Integral Function)分别为
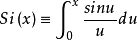 和
和
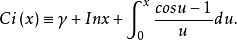 这两个函数与指数积分的关系如下
这两个函数与指数积分的关系如下
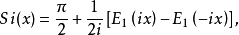
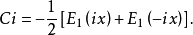 由此可得
由此可得
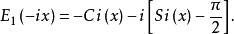 这两个函数的渐近值为1
这两个函数的渐近值为1
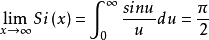 和
和
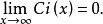
指数积分与其它函数的关系与对数积分
指数积分与对数积分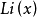 的关系:
的关系: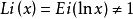 ;另外一个有密切关系的函数:
;另外一个有密切关系的函数: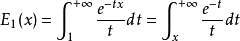 **;**可以延伸到负数:
**;**可以延伸到负数: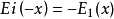 ;我们可以把两个函数都用整函数来表示:
;我们可以把两个函数都用整函数来表示:
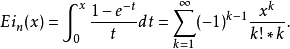
此函数的性质:
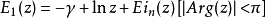 ;
;
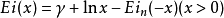 ;
;
指数积分还可以推广为: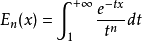 。
。
导数
函数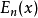 与
与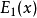 的导数有以下简单的关系:
的导数有以下简单的关系: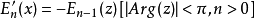 ;然而,这里假设了n是整数;复数n的推广还没有在文献中报导,虽然这种推广是有可能的。
;然而,这里假设了n是整数;复数n的推广还没有在文献中报导,虽然这种推广是有可能的。
复变量的指数积分
从定义中可以看出,指数积分与三角积分之间的关系: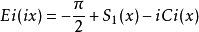 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国