[科普中国]-贝叶斯风险

基本介绍

风险函数给出了一个判断决策函数优劣的标准，诚然，风险函数越小越好，因此，若存在这样一个决策函数d*，使对任何决策函数d都有1

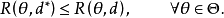则称d*为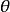 的一致最优决策函数，然而一致最优决策函数通常是不存在的，故有必要引进某种限制较宽的优良性准则。

贝叶斯统计是将参数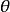 理解成具有先验分布的随机变量，在这个观点下，风险函数 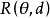便是随机变量，如果再把风险函数 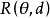对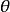 取一次平均，那么所得结果就不依赖于参数 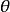而仅依赖于决策函数d了，以此作为衡量决策， 函数优劣的标准应该是合理的。

设参数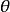 是具有先验分布的随机变量，决策函数d的风险函数为 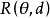，记

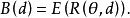其中期望值是对 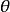求的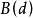， 称为决策函数d在给定先验分布下的贝叶斯风险，简称d的贝叶斯风险。1

从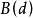 的定义知，可以把贝叶斯风险看做是随机损失函数 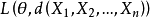求两次期望而得到的，当总体X和参数 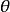都是连续性随机变量时，1

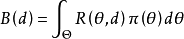
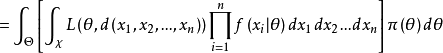
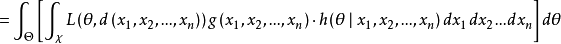
相关概念决策空间与决策函数设总体X的分布函数为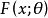 ，用样本空间一个点 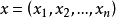对未知参数 作的一个估计，亦即作一个决定，在统计决策中称这一决定为决****策，并称可能采取的全部决策所成的集合为决策空间，记为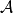

统计决策问题，实质上是对样本空间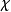 的每一个样本点 ，在决策空间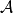 上指明一个点与之对应．这样一个对应规则可以看做定义在样本空间 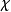上而取值于决策空间 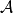的一个函数，称这个函数为决策函数，记为 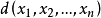．在不至于引起误解的情形下，也称 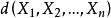为决策函数，这时，表示在得到样本观察值 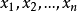时，采取决策 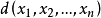．因此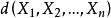 本质上是一个统计**。1**