简介
数学上,称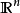 上的实值函数
上的实值函数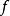 适合赫尔德条件,或称赫尔德连续,当存在非负常数
适合赫尔德条件,或称赫尔德连续,当存在非负常数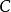 ,
,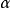 ,使得
,使得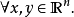 ,
,
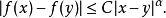
这条件可以推广至任何两个度量空间之间的函数。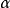 称为赫尔德条件的指数。如果
称为赫尔德条件的指数。如果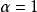 ,则函数适合利普希茨条件。如果
,则函数适合利普希茨条件。如果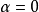 ,则函数不过是有界的。
,则函数不过是有界的。
由适合某个赫尔德条件的函数组成的赫尔德空间,在泛函分析有关解偏微分方程的领域有基本地位。记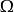 为某个欧几里得空间的开集,赫尔德空间
为某个欧几里得空间的开集,赫尔德空间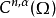 所包含的函数,是直到n阶微分都适合指数
所包含的函数,是直到n阶微分都适合指数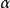 的赫尔德条件。
的赫尔德条件。
赫尔德不等式是数学分析的一条不等式,取名自奥托·赫尔德(Otto Hölder)。这是一条揭示Lp空间的相互关系的基本不等式:
设S为测度空间,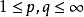 ,及
,及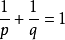 ,设f在
,设f在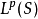 内,g在
内,g在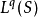 内。则
内。则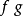 在
在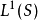 内,且有
内,且有
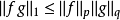 。
。
若S取作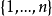 附计数测度,便得赫尔德不等式的特殊情形:对所有实数(或复数)
附计数测度,便得赫尔德不等式的特殊情形:对所有实数(或复数)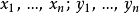 ,有
,有
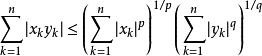 。
。
我们称p和q互为赫尔德共轭。
若取S为自然数集附计数测度,便得与上类似的无穷级数不等式。
当p = q = 2,便得到柯西-施瓦茨不等式。
赫尔德不等式可以证明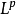 空间上一般化的三角不等式,闵可夫斯基不等式,和证明
空间上一般化的三角不等式,闵可夫斯基不等式,和证明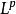 空间是
空间是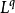 空间的对偶1。
空间的对偶1。
备注在赫尔德共轭的定义中,1/∞意味着零。
如果1 ≤ p,q 和 表示(可能无穷的)表达式:
表示(可能无穷的)表达式:
 以及
以及 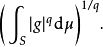
如果p = ∞,那么||f ||∞表示|f |的本性上确界,||g||∞也类似。
在赫尔德不等式的右端,0乘以∞以及∞乘以0意味着 0。把a > 0乘以∞,则得出 ∞1。
证明赫尔德不等式有许多证明,主要的想法是杨氏不等式。
如果||f ||p = 0,那么f μ-几乎处处为零,且乘积fg μ-几乎处处为零,因此赫尔德不等式的左端为零。如果||g||q = 0也是这样。因此,我们可以假设||f ||p > 0且||g||q > 0。
如果||f ||p = ∞或||g||q = ∞,那么不等式的右端为无穷大。因此,我们可以假设||f ||p和||g||q位于(0,∞)内。
如果p = ∞且q = 1,那么几乎处处有|fg| ≤ ||f ||∞ |g|,不等式就可以从勒贝格积分的单调性推出。对于p = 1和q = ∞,情况也类似。因此,我们还可以假设p, q ∈ (1,∞)。
分别用f和g除||f ||p||g||q,我们可以假设:
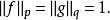
我们使用杨氏不等式:
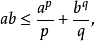
对于所有非负的a和b,当且仅当ap = bq时等式成立。因此:
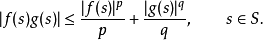
两边积分,得:
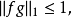
这便证明了赫尔德不等式。
在p ∈ (1,∞)和||f ||p = ||g||q = 1的假设下,等式成立当且仅当几乎处处有|f |p = |g|q。更一般地,如果||f ||p和||g||q位于(0,∞)内,那么赫尔德不等式变为等式,当且仅当存在α, β > 0(即α = ||g||q且β = ||f ||p),使得:
 。
。
例子如果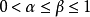 ,那么所有
,那么所有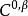 赫尔德连续函数都是
赫尔德连续函数都是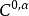 赫尔德连续的。这也包括了
赫尔德连续的。这也包括了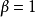 (这里需要集合是有界的),所以所有利普希茨连续函数都是
(这里需要集合是有界的),所以所有利普希茨连续函数都是 赫尔德连续。
赫尔德连续。
在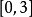 上定义函数
上定义函数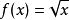 ,
,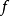 不是利普希茨连续;但对
不是利普希茨连续;但对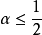 ,
,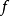 是
是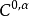 赫尔德连续。2
赫尔德连续。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国