知识详解
在平面上取一定点O,从O引一条水平射线 ,规定方向自左至右,再选定一个长度单位并规定角旋转的正方向,通常取逆时针方向,这样就构成了一个极坐标系,如图1所示,点O叫作极点,射线
,规定方向自左至右,再选定一个长度单位并规定角旋转的正方向,通常取逆时针方向,这样就构成了一个极坐标系,如图1所示,点O叫作极点,射线 叫作极轴。2
叫作极轴。2
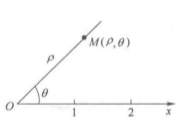
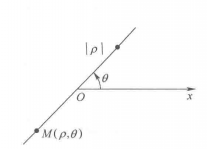
在极坐标系中,平面上任意一点M的位置,可以由OM的长度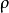 和从
和从 到OM的角
到OM的角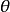 来确定,把
来确定,把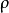 叫作点M的极径,
叫作点M的极径,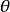 叫作点M的极角,有序实数对
叫作点M的极角,有序实数对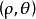 叫作点M的极坐标,记作
叫作点M的极坐标,记作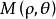 。
。
特别地,当点M在极点时,它的坐标是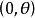 ,
,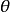 可以取任意值,当点M在极轴上时,它的坐标是
可以取任意值,当点M在极轴上时,它的坐标是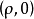 ,
,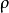 可以取任意正值。2
可以取任意正值。2
如图2所示,在极坐标系中,点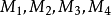 的极坐标分别为
的极坐标分别为 。
。
在实际应用时,极径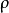 和极角
和极角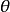 也可以取负值,当
也可以取负值,当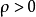 时,点
时,点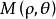 在
在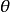 的终边上取一点,使
的终边上取一点,使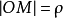 ,当
,当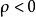 时,点
时,点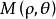 在角
在角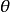 终边的反向延长线上取一点,使
终边的反向延长线上取一点,使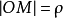 ,如图3所示,当极轴按顺时针方向旋转时,
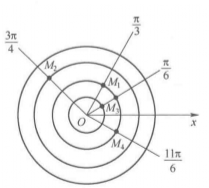
,如图3所示,当极轴按顺时针方向旋转时, .在如图4所示的极坐标系中,点
.在如图4所示的极坐标系中,点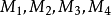 的极坐标分别为
的极坐标分别为 。
。

由此可见,对于任意给定的一对实数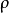 和
和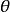 ,在平面上就有唯一确定的点
,在平面上就有唯一确定的点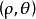 与之相对应,反过来,平面上任意一点的极坐标却可以有无数多种表示法,图4中的点
与之相对应,反过来,平面上任意一点的极坐标却可以有无数多种表示法,图4中的点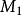 的极坐标还可以表示为
的极坐标还可以表示为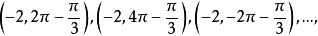 这里
这里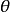 相差
相差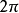 的整数倍,因此,平面上的点和它的极坐标
的整数倍,因此,平面上的点和它的极坐标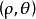 的关系不是一一对应的,为了使点M(极点除外)的极坐标能唯一确定,一般取
的关系不是一一对应的,为了使点M(极点除外)的极坐标能唯一确定,一般取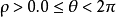 。2
。2
极坐标和直角坐标的互化极坐标系和直角坐标系是两种不同的坐标系,同一个点既可以用极坐标表示,也可以用直角坐标表示。把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图5所示,设M是平面内任意一点,它的直角坐标是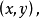 极坐标是
极坐标是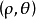 ,显然有
,显然有
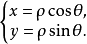
利用上式,可以把点M的极坐标化为直角坐标。
由上面的公式,又可得
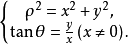
利用该公式,可以把点M的直角坐标化为极坐标。2
例题解析例1 把点M的极坐标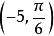 化为直角坐标。
化为直角坐标。
解: 由公式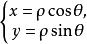 得
得
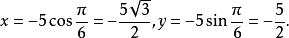 于是得点M的直角坐标为
于是得点M的直角坐标为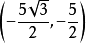 。
。
例2 把点M的直角坐标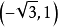 化为极坐标。
化为极坐标。
**解:**由公式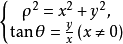 得
得
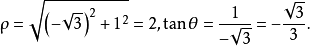 因为点M在第二象限,所以
因为点M在第二象限,所以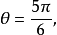 于是得点M的极坐标为
于是得点M的极坐标为 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国