[科普中国]-等角螺线

定义

等角螺线、对数螺线或生长螺线是在自然界常见的螺线，在极坐标系(r, θ)中，这个曲线可以写为

或

因此叫做“对数”螺线

定理 推出： ，推出：角 。设 C 为以原点为圆心的任意圆，则 C 与等角螺线的相交的角永远相等，而此值为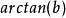 ，名为「倾斜度」

等角螺线是自我相似的；这即是说，等角螺线经放大后可与原图完全相同。

等角螺线的渐屈线和垂足线都是等角螺线。

从原点到等角螺线的任意点上的长度有限，但由该任意点出发沿等角螺线走到原点却需绕原点转无限次。这是由 Torricelli 发现的。（指数函数的取值范围为负无穷到正无穷，x轴是渐近线，因此极径r永远不会等于0，也即无法到达原点o）1

建造等角螺线在复平面上定义一个复数 ，其中 ，那么连起 z、z²、z³…… 的曲线就是一条等角螺线。

若 L 是复平面中的一条直线且不平行于实数或虚数轴，那么指数函数 ez 会将这些直线映像到以 0 为中心的等角螺线。

使用黄金长方形：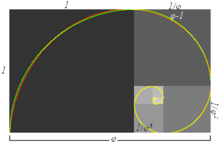

自然现象鹦鹉螺的贝壳像等角螺线

菊的种子排列成等角螺线

鹰以等角螺线的方式接近它们的猎物

昆虫以等角螺线的方式接近光源

蜘蛛网的构造与等角螺线相似

旋涡星系的旋臂差不多是等角螺线。银河系的四大旋臂的倾斜度约为 12°。

低气压(热带气旋、温带气旋等)的外观像等角螺线2

历史等角螺线是由笛卡儿在1638年发现的。雅各布．伯努利后来重新研究之。他发现了等角螺线的许多特性，如等角螺线经过各种适当的变换之后仍是等角螺线。他十分惊叹和欣赏这曲线的特性，故要求死后将之刻在自己的墓碑上，并附词「纵使改变，依然故我」(eadem mutata resurgo)。可惜雕刻师误将阿基米德螺线刻了上去3。

等角螺线又称为对数螺线。