基本概念
我们将研究对象的全体组成的集合称为总体(population),而把组成总体的元素称为个体(individual),总体与个体之间的关系,即集合与元素的关系。
例如,研究一批灯泡的寿命,则整批灯泡的寿命组成的集合就是总体,每一个灯泡的寿命就是一个个体。又如,研究某班学生的高等数学期末考试成绩时,该班全体学生的考试分数就是总体,其中每个学生的考试成绩就是该总体中的个体。
在数理统计中,我们经常研究的是总体中各个个体的一项或几项数量指标和该指标在总体中的分布情况。用X表示数量指标,则指标值X随个体不同而变化。由于在统计问题中,从总体中抽取个体是随机抽取的,因此,X是一个随机变量,这样,从数学意义来说,总体可以作为随机变量X所有可能取值的全体,个体就是其中的一个具体值,因而随机变量X的分布就完全描述了总体中所研究的数量指标的分布情况,我们把总体与数量指标X可能取值的全体所组成的集合等同起来,用随机变量X表示,总体的分布就是指随机变量X的分布。
总体X作为一个随机变量有一维与多维,连续型与离散型之分,而作为一个集合,则区分为有限总体与无限总体.
例如,某工厂一季度生产的电子元件寿命所构成的总体中,个体的总数就是一季度生产的电子元件数,这就是一个有限总体,而该工厂生产的所有电子元件的寿命所构成的总体是一个无限总体,在实际问题中,当有限总体所包含的个体的总数很大时,可以认为它是无限总体。1
定义1 把研究对象的全体(通常为数量指标X可能取值的全体组成的集合)称为总****体,总体中的每个元素称为个体。1
总体分布的检验检验时,若总体分布的形式是已知的,只是要对分布中一些未知参数做检验.就是参数检验****。但是,有时情况并非如此,在有些问题中,总体服从什么分布是未知的,我们的任务,就是要对总体是否服从某个分布做检验.这样的检验称为总体分布的检验。它是一种非参数检验。
不含未知参数的总体分布的检验有一种非参数估计方法,即用频率直方图来估计总体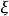 的分布.它的做法是:作分点
的分布.它的做法是:作分点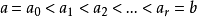 ,将
,将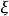 的取值范同[a,b]分成r个区间.设共进行了n次试验,落在区间
的取值范同[a,b]分成r个区间.设共进行了n次试验,落在区间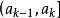 中的样本观测值的个数为
中的样本观测值的个数为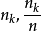 为频率,在每一个区间
为频率,在每一个区间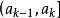 上,以
上,以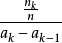 为高度,作长方形,这样得到由一排长方形构成的频率直方图。
为高度,作长方形,这样得到由一排长方形构成的频率直方图。
设 是总体
是总体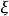 落在区间
落在区间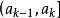 中的概率,由于样本落在区间
中的概率,由于样本落在区间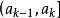 中的频率≈总体落在因司
中的频率≈总体落在因司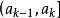 中的概率,所以,有
中的概率,所以,有 。
。
现在的问题是要检验总体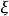 是否服从某个已知的分布
是否服从某个已知的分布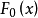 ,一方面,可以从
,一方面,可以从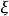 的样本求出
的样本求出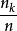 ;另一方面,可以从
;另一方面,可以从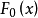 求出
求出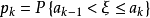 ,如果
,如果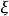 服从
服从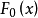 ,则有
,则有 ,即有
,即有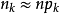 ;如果
;如果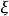 不服从
不服从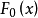 ,则
,则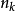 与
与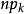 的差别就会很大,正是从这一思想出发,产生了下列检验一个总体是否服从某个已知分布的一种检验方法。
的差别就会很大,正是从这一思想出发,产生了下列检验一个总体是否服从某个已知分布的一种检验方法。
问题 设 是总体
是总体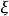 的样本落在区间
的样本落在区间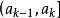 中的频数(k=1,2,…,r),要检验
中的频数(k=1,2,…,r),要检验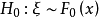 ,其中,
,其中,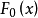 是某个已知的不含未知参数的分布。
是某个已知的不含未知参数的分布。
检验方法
从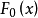 求出
求出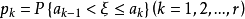 ,可以证明,若
,可以证明,若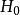 为真,则当
为真,则当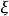 的样本观测次数
的样本观测次数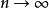 时,有
时,有
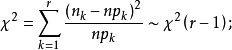 若
若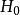 不真,则
不真,则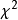 的值会偏大,统计量
的值会偏大,统计量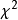 的分布,相对于
的分布,相对于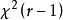 分布来说,峰值位置会有一个向右的偏移。
分布来说,峰值位置会有一个向右的偏移。
因此可得到检验方法如下:对于给定的显著水平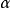 ,自由度r-1,查表可得
,自由度r-1,查表可得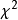 分布的临界值
分布的临界值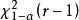 ,使得
,使得 ,从样本求出
,从样本求出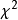 的值.当
的值.当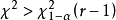 时拒绝
时拒绝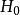 ;否则接受
;否则接受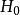 。
。
注意:
(1)查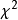 分布表求临界值时,在自由度k=r-1与
分布表求临界值时,在自由度k=r-1与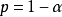 相交处查得
相交处查得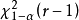 ;
;
(2)为了保证检验结果比较可靠,最好有n≥50,nk≥5(k=1,2,…,r),如果有一些nk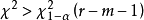 时拒绝
时拒绝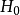 ;否则接受
;否则接受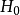 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国