[科普中国]-比例系数

正比例中的比例系数

正比例：两种相关联的量，当一种量的任意两个数值的比，等于另一种量对应的两个数值的比，那么这样的两种量就叫做成正比例的量。用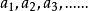表示量A的值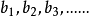，表示量B的对应值，如果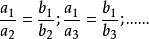那么A、B两种量就是成正比例的量。

因为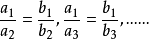

显然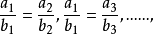

所以。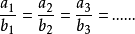

由此可以看出，这些比的比值相等。

用y和x表示两种相互关联的量，如果这两种量中相对应的两个数的比值一定，那么y和x就成正比例。用k表示比值，这个关系可以表示成：

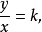或者

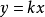
常数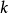叫做比例系数。1

反比例中的比例系数两种相关联的量，当一种量的任意两个数值的比，等于另一种量对应的两个数值的反比，那么这样的两种量就叫做成反比例的量，用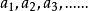表示量A的值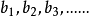．表示量B的对应值，如果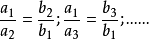那么A、B两种量就是成反比例的量。

由此可看出，。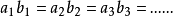

用y和x表示两种量，如果这两种量中相对应的两个数值的积一定，那么y和x就成反比例，用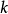表示这个积，这个关系可以表示为：

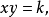或者

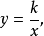常数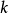也叫做比例系数。1

关于物理单位的比例系数在物理学的方程式中都包含有比例系数，所包含的比例系数与单位的选择有关。在定义方程式中，包含的比例系数是一个永远无量纲的量，它的数值是表示被量度的量的一种单位比另一种单位大到多少倍。例如，若方程中所有各量均用一种制的单位来表示，则此例系数等于1，若各量是用不同单位制表示，则系数不等于1。速度公式

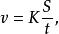所以

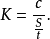
当S用厘米、t用秒、v用千米/小时表示，则 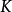=(千米/小时)/(厘米/秒)=。

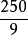当S用米、t用秒、v用千米/分表示，则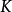=(千米/分)/(厘米/秒)=。

所以为了避免因系数而招致的麻烦，所有包含在一个公式中的量，在计算时要用同一种单位制来表示，计算结果也将是同一单位制，此例系数(K=1)可以略去不写。2

大多数物理学方程式，属于定义方程式之列，在少数本来也可以成为定义方程式而不属于定义方程式的物理学公式中，其比例系数是用实验方法测定的，它是一个不等于1、有量纲、而且是具有一定物理意义的常数。例如万有引力定律

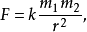
由子力的单位已经由牛顿第二定律作了规定，于是万有引力定律虽然也是表示力，就不能成为力的单位的定义方程式。因此公式中的此例系数k就不能等于1，而且还有量纲。1798年开文迪许第一次测定了它的数值，称为引力常数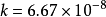：厘米3克-1秒-2，它表示质量各为1克、相距1厘米的两质点，相互作用力的大小值。

还有克拉珀龙定律公式，可写成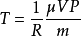。由于在历史上温度的单位是独立选定的，所以不能令R等于1。这一个被称为普适气体常数的系数，也是用实验的方法测定的。其量纲式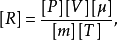它表明一克分子理想气体，当温度升高1℃时，在等压膨胀的情况下所作的功的大小。2