[科普中国]-非线性方程

定义

在数学上，一个线性函数（映射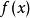） 拥有以下两个性质：

叠加性： ；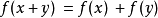

齐次： 。

在α是有理数的情况下，一个可叠加函数必定是齐次函数（在讨论线性与否时，齐次函数专指一次齐次函数）；若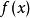 是连续函数，则只要α是任意实数，就可以从叠加性推出齐次。然而在推广至任意复数α时，叠加性便再也无法导出齐次了。也就是说，在复数的世界里存在一种反线性映射，它满足叠加性，但却非齐次。叠加性和齐次这两个条件常会被合并在一起，称之为叠加原理：

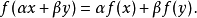
对于一个表示为

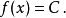
的方程，如果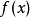 是一个线性映射，则称为线性方程，反之则称为非线性方程。另外，如果 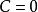，则称此方程齐次（齐次在函数和方程上的定义不同，齐次方程指方程内没有和x无关的项C，即任何项皆和x有关）。

这里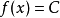 的定义是很一般性的， 可为任何数字、向量、函数等，而 可以指任意映射，例如有条件限制（给定初始值或边界值）的微分或积分运算。如果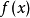 内含有对 的微分运算，此方程即是一个微分方程1。

分类这些方程可分为两类，一种是多项式方程，一种是非多项式方程。

非线性代数方程主条目：代数方程

主条目：多项式

代数方程又称为多项式方程。令某多项式等于零可得一个多项式方程，例如：

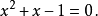
利用勘根法可以找出某个代数方程的解；但若是代数方程组则较为复杂，有时候甚至很难确定一个代数方程组是否具有复数解（见希尔伯特零点定理）。即使如此，对于一些具有有限个复数解的多项式方程组而言，我们已经找到解的方法，并且也已充分了解这种系统的行为。代数方程组的研究是代数几何里重要的一环，而代数几何正是现代数学里的其中一个分枝2。

非线性微分方程若描述一个系统的微分方程是非线性的，则称此系统为非线性系统。含有非线性微分方程的问题，系统彼此间的表现差异极大，而每个问题的解法或是分析方法也都不一样。非线性微分方程的例子如流体力学的纳维-斯托克斯方程，以及生物学的洛特卡－沃尔泰拉方程。

解非线性问题最大的难处在于找出未知的解：一般来说，我们无法用已知的解来拼凑出其他满足微分方程的未知解；而在线性的系统里，却可以利用一组线性独立的解，透过叠加原理组合出此系统的通解。例如满足狄利克雷边界条件的一维热传导问题，其解（时间的函数）可以写成许多不同频率之正弦函数的线性组合，而这也让它的解很弹性、具有很大的变化空间。通常我们可以找到非线性微分方程的特解，但由于此时叠加原理并不适用，故无法利用这些特解来建构出其他新的解3。

常微分方程一阶常微分方程常常可以利用分离变数法来解，特别是自守方程

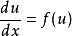
例如

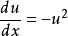
这个方程式的通解为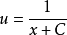 ，特解为u= 0（即通解在C趋近于无限大时的极限）。此方程是非线性的，因为它可以被改写为

，

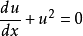而等号左边并不是u的线性映射。若把此式的u换成u，则会变成线性方程（指数衰减）。

二阶和高阶非线性常微分方程组的解几乎无法表示成解析解，反而较常表为隐函数或非初等函数积分的形式。

分析常微分方程常用的方法包括：

检查是否有任何守恒量（特别是在处理哈密顿系统的时候）。

检查有没有类似守恒量的耗散量（见李亚普诺夫函数）。

利用泰勒展开式作线性近似。

利用变数变换法，改写成较易分析的方程。

分岔理论。

微扰法（也可应用在代数方程上）1。

偏微分方程参见：非线性偏微分方程列表

研究非线性偏微分方程最常见也最基础的方法就是变数变换，变换以后的方程会较简单，甚至有可能会变成线性方程。有时候，变数变换后的方程可能会变成一个或两个以上的常微分方程（如同用分离变数法解偏微分方程），不管这些常微分方程可不可解，都能帮助我们了解这个系统的行为。

另一个流体力学和热力学里常用的方法（但数学性较低），是利用尺度分析来简化一个较一般性的方程，使它仅适用在某个特定的边界条件上。例如，在描述一个圆管内一维层流的暂态时，我们可以把非线性的纳维-斯托克斯方程简化成一个线性偏微分方程；这时候尺度分析提供了两个特定的边界条件：一维和层流。

其他分析非线性偏微分方程的方法还有特征线法，以及上述分析常微分方程时常用的方法2。

单摆主条目：单摆

单摆（v 表示速度向量；a 表示加速度向量）

非线性问题的一个典型的例子，就是重力作用之下单摆的运动。单摆的运动可由以下的方程来描述（用拉格朗日力学可以证明）：

。

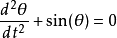这是一个非线性且无因次的方程， 是单摆和它静止位置所夹的角度，如动画所示。此方程的一个解法是将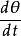 视为积分因子，积分以后得

。

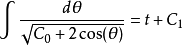上述的解是隐解的形式，同时也包含了椭圆积分。这个解通常没有什么用，因为非初等函数积分（即使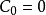仍然是非初等函数）把解的各种特性隐藏了起来，使我们不易看出单摆系统的行为。

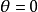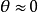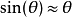另一个解法是把这个非线性方程作线性近似：利用泰勒展开式将非线性的 sine 函数线性化，并在某些特定的点附近讨论解的情形。例如，若在 的点附近作线性近似（又称小角度近似）， 时， ，故原方程可以改写为

。

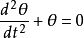近似后的方程变成了简谐振荡，因此当单摆运动到底部附近时，可以对应到一个简谐振子。而若在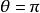（即当单摆运动到圆弧的最高点时）附近作线性近似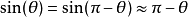，，故原方程可以改写为

。

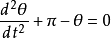这个方程的解含有双曲正弦函数，因此和小角度近似不同，这个近似是不稳定的，也就是说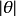会无限制地增加（但此近似方程的解也可能是有界的）。当我们把解对应回单摆系统后，就可以了解为什么单摆在圆弧的最高点时不能达到稳定平衡，也就是说，单摆在最高点时是不稳定的状态。

另一个有趣的线性近似是在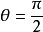 附近，此时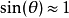，故原方程可以改写为

，

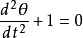这个近似后的方程可以对应到自由落体。

若把以上线性近似的结果合在一起看，就能大致了解单摆的运动情形。利用其他解非线性微分方程的方法，可以进一步帮助我们找到更精确的相图，或是估算单摆的周期2。

发展史十一世纪前1086～1093年，中国宋朝的沈括在《梦溪笔谈》中提出“隙积术”和“会圆术”，开始高阶等差级数的研究。

十一世纪十一世纪，阿拉伯的阿尔·卡尔希第一次解出了二次方程的根。

十一世纪，阿拉伯的卡牙姆完成了一部系统研究三次方程的书《代数学》。

十一世纪，埃及的阿尔·海赛姆解决了“海赛姆”问题，即要在圆的平面上两点作两条线相交于圆周上一点，并与在该点的法线成等角。

十一世纪中叶，中国宋朝的贾宪在《黄帝九章算术细草》中，创造了开任意高次幂的“增乘开方法”，并列出了二项式定理系数表，这是现代“组合数学”的早期发现。后人所称的“杨辉三角”即指此法1。

十三世纪十三世纪，印度的拜斯迦罗著《立刺瓦提》一书，这是东方算术和计算方面的重要著作。

1202年，意大利的裴波那契发表《计算之书》，把印度—阿拉伯记数法介绍到西方。

1220年，意大利的裴波那契发表《几何学实习》一书，介绍了许多阿拉伯资料中没有的示例。

1247年，中国宋朝的秦九韶著《数书九章》共十八卷，推广了“增乘开方法”。书中提出的联立一次同余式的解法，比西方早五百七十余年。

1248年，中国宋朝的李治著《测圆海镜》十二卷，这是第一部系统论述“天元术”的著作。

1261年，中国宋朝的杨辉著《详解九章算法》，用“垛积术”求出几类高阶等差级数之和。

1274年，中国宋朝的杨辉发表《乘除通变本末》，叙述“九归”捷法，介绍了筹算乘除的各种运算法。

1280年，元朝《授时历》用招差法编制日月的方位表(中国 王恂、郭守敬等)。

十四世纪中叶前，中国开始应用珠算盘。

十四世纪1303年，中国元朝的朱世杰著《四元玉鉴》三卷，把“天元术”推广为“四元术”。

十五世纪1464年，德国的约·米勒在《论各种三角形》(1533年出版)中，系统地总结了三角学。

1494年，意大利的帕奇欧里发表《算术集成》，反映了当时所知道的关于算术、代数和三角学的知识。

十六世纪1545年，意大利的卡尔达诺、费尔诺在《大法》中发表了求三次方程一般代数解的公式。

1550～1572年，意大利的邦别利出版《代数学》，其中引入了虚数，完全解决了三次方程的代数解问题。

1591年左右，德国的韦达在《美妙的代数》中首次使用字母表示数字系数的一般符号，推进了代数问题的一般讨论。

1596～1613年，德国的奥脱、皮提斯库斯完成了六个三角函数的每间隔10秒的十五位小数表。

十七世纪1614年，英国的耐普尔制定了对数。

1615年，德国的开卜勒发表《酒桶的立体几何学》，研究了圆锥曲线旋转体的体积。

1635年，意大利的卡瓦列利发表《不可分连续量的几何学》，书中避免无穷小量，用不可分量制定了一种简单形式的微积分。

1637年，法国的笛卡尔出版《几何学》，提出了解析几何，把变量引进数学，成为“数学中的转折点”。

1638年，法国的费尔玛开始用微分法求极大、极小问题。

1638年，意大利的伽里略发表《关于两种新科学的数学证明的论说》，研究距离、速度和加速度之间的关系，提出了无穷集合的概念，这本书被认为是伽里略重要的科学成就。

1639年，法国的迪沙格发表了《企图研究圆锥和平面的相交所发生的事的草案》，这是近世射影几何学的早期工作。

1641年，法国的帕斯卡发现关于圆锥内接六边形的“帕斯卡定理”。

1649年，法国的帕斯卡制成帕斯卡计算器，它是近代计算机的先驱。

1654年，法国的帕斯卡、费尔玛研究了概率论的基础。

1655年，英国的瓦里斯出版《无穷算术》一书，第一次把代数学扩展到分析学。

1657年，荷兰的惠更斯发表了关于概率论的早期论文《论机会游戏的演算》。

1658年，法国的帕斯卡出版《摆线通论》，对“摆线”进行了充分的研究。

1665～1676年，牛顿(1665～1666年)先于莱布尼茨(1673～1676年)制定了微积分，莱布尼茨(1684～1686年)早于牛顿(1704～1736年)发表了微积分。

1669年，英国的牛顿、雷夫逊发明解非线性方程的牛顿—雷夫逊方法。

1670年，法国的费尔玛提出“费尔玛大定理”。

1673年，荷兰的惠更斯发表了《摆动的时钟》，其中研究了平面曲线的渐屈线和渐伸线。

1684年，德国的莱布尼茨发表了关于微分法的著作《关于极大极小以及切线的新方法》。

1686年，德国的莱布尼茨发表了关于积分法的著作。

1691年，瑞士的约·贝努利出版《微分学初步》，这促进了微积分在物理学和力学上的应用及研究。

1696年，法国的洛比达发明求不定式极限的“洛比达法则”。

1697年，瑞士的约·贝努利解决了一些变分问题，发现最速下降线和测地线。

十八世纪1704年，英国的牛顿发表《三次曲线枚举》《利用无穷级数求曲线的面积和长度》《流数法》。

1711年，英国的牛顿发表《使用级数、流数等等的分析》。

1713年，瑞士的雅·贝努利出版了概率论的第一本著作《猜度术》。

1715年，英国的布·泰勒发表《增量方法及其他》。

1731年，法国的克雷洛出版《关于双重曲率的曲线的研究》，这是研究空间解析几何和微分几何的最初尝试。

1733年，英国的德·勒哈佛尔发现正态概率曲线。

1734年，英国的贝克莱发表《分析学者》，副标题是《致不信神的数学家》，攻击牛顿的《流数法》，引起所谓第二次数学危机。

1736年，英国的牛顿发表《流数法和无穷级数》。

1736年，瑞士的欧拉出版《力学、或解析地叙述运动的理论》，这是用分析方法发展牛顿的质点动力学的第一本著作。

1742年，英国的麦克劳林引进了函数的幂级数展开法。

1744年，瑞士的欧拉导出了变分法的欧拉方程，发现某些极小曲面。

1747年，法国的达朗贝尔等由弦振动的研究而开创偏微分方程论。

1748年，瑞士的欧拉出版了系统研究分析数学的《无穷分析概要》，这是欧拉的主要著作之一。

1755～1774年，瑞士的欧拉出版了《微分学》和《积分学》三卷。书中包括微分方程论和一些特殊的函数。

1760～1761年，法国的拉格朗日系统地研究了变分法及其在力学上的应用。

1767年，法国的拉格朗日发现分离代数方程实根的方法和求其近似值的方法。

1770～1771年，法国的拉格朗日把置换群用于代数方程式求解，这是群论的开始。

1772年，法国的拉格朗日给出三体问题最初的特解。

1788年，法国的拉格朗日出版了《解析力学》，把新发展的解析法应用于质点、刚体力学。

1794年，法国的勒让德出版流传很广的初等几何学课本《几何学概要》。

1794年，德国的高斯从研究测量误差，提出最小二乘法，于1809年发表。

1797年，法国的拉格朗日发表《解析函数论》，不用极限的概念而用代数方法建立微分学。

1799年，法国的蒙日创立画法几何学，在工程技术中应用颇多。

1799年，德国的高斯证明了代数学的一个基本定理：实系数代数方程必有根4。

求解如何求解第一类多项式方程，已经有了比较成熟的理论和方法。比较常用的一种数值方法是迭代法，他能够通过迭代次数的增加，而越来越接近方程的解。

至于如何求解第二类非多项式方程，是数学领域中的一个重点研究方向。一般来说，求解此类方程是采用随机搜索的办法5。