定义
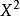 在数论中,特别在同余理论里,一个整数
在数论中,特别在同余理论里,一个整数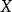 对另一个整数
对另一个整数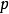 的二次剩余(英语:Quadratic residue)指
的二次剩余(英语:Quadratic residue)指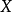 的平方除以
的平方除以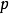 得到的余数。
得到的余数。
当存在某个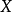 ,式子
,式子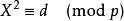 成立时,称
成立时,称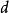 是模
是模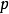 的二次剩余****”
的二次剩余****”
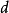 当对任意
当对任意 ,
,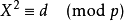 不成立时,称**“是模
不成立时,称**“是模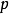 的二次非剩余****”**
的二次非剩余****”**
研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用,包括从噪音工程学到密码学以及大数分解。
研究历史以及基本概念从17世纪到18世纪,费马、欧拉、拉格朗日和勒让德等数论学家对二次剩余理论作了初步的研究,证明了一些定理并作出了一些相关的猜想,但首先对二次剩余进行有系统的研究的数学家是高斯。他在著作《算术研究》(Disquisitiones Arithmeticae,1801年)中首次引入了术语“二次剩余”与“二次非剩余”,并声明在不至于导致混淆的行文中,可以省略“二次”两字1。
基本结论质数二次非剩余对于质数2,每个整数都是它的二次剩余。
以下讨论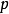 是奇质数的情况:
是奇质数的情况:
对于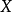 ,
,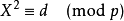 而言,能满足“
而言,能满足“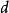 是模
是模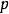 的二次剩余”的
的二次剩余”的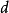 共有
共有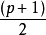 个(剩余类),分别为:
个(剩余类),分别为:
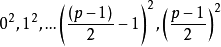 (0计算在内)
(0计算在内)
此外是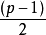 个二次非剩余。但在很多情况下,我们只考虑乘法群Z/pZ,因此不将0包括在内。这样,每个二次剩余的乘法逆元仍然是二次剩余;二次非剩余的乘法逆元仍然是二次非剩余。二次剩余的个数与二次非剩余的个数相等,都是
个二次非剩余。但在很多情况下,我们只考虑乘法群Z/pZ,因此不将0包括在内。这样,每个二次剩余的乘法逆元仍然是二次剩余;二次非剩余的乘法逆元仍然是二次非剩余。二次剩余的个数与二次非剩余的个数相等,都是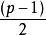 。此外,两个二次非剩余的乘积是二次剩余,二次剩余和二次非剩余的乘积是二次非剩余。
。此外,两个二次非剩余的乘积是二次剩余,二次剩余和二次非剩余的乘积是二次非剩余。
应用二次互反律可以知道,当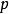 模4余1时,-1是
模4余1时,-1是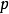 的二次剩余;如果
的二次剩余;如果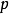 模4余3,那么,-1是
模4余3,那么,-1是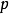 的二次非剩余。
的二次非剩余。
要知道d是否为模p的二次剩余,可以运用欧拉判别法(或叫欧拉准则)。
合数二次非剩余首先可以看出,
如果a是模n的剩余,并且p整除n,那么a是模p的剩余。
如果a是模n的非剩余,那么存在p整除n,使得a是模p的非剩余。
对于模合数的情况,两个剩余的乘积仍然是剩余,剩余和非剩余的乘积必为非剩余,但是两个非剩余的乘积则可能是剩余、非剩余或0。
比如,对于模15的情况
1, 2, 3,4, 5,6, 7, 8,9,10, 11, 12, 13, 14(粗斜体为二次剩余)。
两个二次非剩余2和8的乘积是二次剩余1,但另外两个二次非剩余2和7的乘积是二次非剩余142。
相关记号高斯使用R和N来分别表示二次剩余及二次非剩余。例如:2 R 7,5 N 7,并且1 和5 R 8,3和7 N 8。尽管这种记号在某些方面来说十分简洁,但现今最常用的是勒让德符号,或称二次特征(见狄利克雷特征)。对于整数a及奇质数p,
|| ||
之所以将0另分一类有两个原因。首先,这使公式和定理叙述方便。其次,二次特征是一个从乘法群Z/pZ射到复数域的群同态,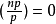 可以将这个同态扩张到整数构成的乘法半群。
可以将这个同态扩张到整数构成的乘法半群。
相比高斯的记号,勒让德符号的优势在于可以写在公式里(作为一个数字值)。此外勒让德符号可以推广到三次以至高次剩余。
勒让德符号中的分母只限奇质数,对于一般的合数,有推广的雅可比符号。雅可比符号的性质比前者复杂。如果aRm那么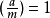 ,如果
,如果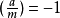 那么aNm。但如果
那么aNm。但如果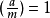 ,我们不能知道aRm还是aNm3。
,我们不能知道aRm还是aNm3。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国