[科普中国]-极限定理

简介

关于随机变量列在一定收敛意义下收敛于某随机变量的定理的总称，包括大数定律、小数定律、中心极限定理、局部极限定理等。

随机变量、分布函数列(概率分布列、特征函数列……)在一定意义下收敛于某随机变量、分布函数(概率分布、特征函数……)的有关定理的总称，主要包括大数定律、小数定律、重对数定律、中心极限定理、局部极限定理……1

以大数定理和中心极限定理为核心的极限定理是概率论的基本理论之 一，它们在概率论与数理统计的理 论研究与应用中都具有十分重要的意义。

大数定律定义在概率论中，用来阐明大量平均结果稳定性的一系列定理统称为大数定律。

中心极限定律定义在客观实际中有许多随机变量，它们是由大量相互独立的随机因素的综合效应所形成的，而其中的每一个单个因素在总的效应中所起的作用都是微小的。这类随机变量往往近似地服从正态分布。在概率论中，论证随机变量和的极限分布是正态分布的一系列定理统称为中心极限定理。

定理切比雪夫不等式设随机变量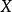 有数学期望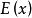和方差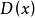，则对于任意给定的正数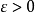,总成立不等式

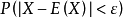
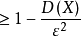
或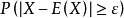

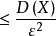
此不等式称为切比雪夫不等式。

由切比雪夫不等式可以看出，若方差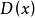越小，则概率 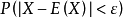越大，表明随机变量 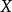取值越集中；反之，方差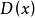越大，概率 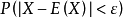越小，表明随机变量 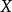取值较分散。

大数定律定理1（切比雪夫定理的特殊情况）设随机变量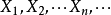相互独立，且具有相同的有限数学期望和方差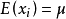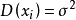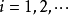：，（）。作前n 个随机变量的算术平均，记为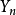

即，则对于任意正数，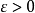

恒有

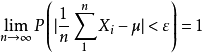
式中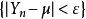，是一个随机事件，等式表明，当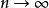时，这个事件的概率趋于1，即对于任意正数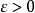，当n 充分大时，不等式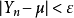几乎都是成立的。通常我们称序列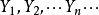依概率收敛于 。

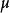一般地，设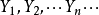为一个随机变量序列，a 是一个常数，若对于任意正数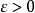都有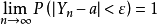

则称随机变量序列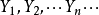依概率收敛于a 。

定理1 表明，当n 很大时，随机变量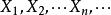的算术平均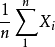接近于数学期望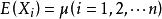,这种接近是概率意义下的接近。2

证明方法这个大数定律的证明确实有几种不同的方法。最早的证明是由数学大师Kolmogorov给出的。Durrett (2010)的书上用的是Etemadi (1981)的方法，需要截断X，用到现代概率论的知识如Borel-Cantelli引理、Kolmogorov三级数定理、Fubini定理等。（感谢读者指出，Durrett的书在倒向鞅一章中给出了大数定律的倒向鞅方法证明，只需要用到倒向鞅的知识和Hewitt-Savage 0-1律，不过这也是现代概率论的知识。）

此外，还有很多不同的大数定律，不同分布的，不独立的序列等。定律也不一定是关于随机变量的，也可以是关于随机函数的，甚至随机集合的等等。以数学家命名的也有Khinchin大数定律(不独立序列的强大数定律)、Chebyshev大数定律(弱大数定律(1))、Poisson大数定律(不同概率的随机事件序列的大数定律)、Bernoulli大数定律(随机事件的大数定律)、Kolmogorov大数定律(强大数定律(6))等等……

中心极限定理定理2 （同分布的中心极限定理）设随机变量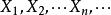相互独立，服从同一分布并且具有有限的数学期望和方差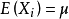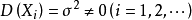，,则随机变量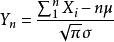的分布函数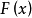对任意的x，满足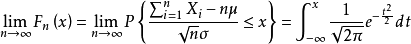

在很多问题中，所考虑的随机变量，都可表示成若干独立的随机变量之和。它们往往近似地服从正态分布。在后面将学的数理统计中，我们会看到，中心极限定理是大样本统计 推断的理论基础。2

应用中心极限定理是概率论中最重要的一类定理，它支撑着和置信区间相关的T检验和假设检验的计算公式和相关理论。如果没有这个定理，之后的推导公式都是不成立的。

事实上，以上对于中心极限定理的两种解读，在不同的场景下都可以对A/B测试的指标置信区间判定起到一定作用。

对于属于正态分布的指标数据，我们可以很快捷地对它进行下一步假设检验，并推算出对应的置信区间；而对于那些不属于正态分布的数据，根据中心极限定理，在样本容量很大时，总体参数的抽样分布是趋向于正态分布的，最终都可以依据正态分布的检验公式对它进行下一步分析。

总结综上所述，通俗的说，大量随机变量的平均值已不具有显著的随机性，而是必然接近 某个常数，这是自然界一类随机现象隐含 的最重要的规律之一；另一规律是，尽管 个别随机变量的分布函数可能各式各样， 但大量相互独立的随机变量和的分布不再 是任意的，而是服从正态分布。2