[科普中国]-对称关系

对称的关系

亦你“具有对称性的关系”。对于类k中一个确定的关系R来说，类k中的任意两个个体x，y， 如果xRy真yRx就必真，则称关系R为类k中对称的关系（对称关系）， 如果xRy真yRx就必假， 则称关系R为类K中反对称的关系（反对称关系）；如果对于某些个体x，y， xRy真同时yRx也真， 而对于另外的个体x，y，xRy真时yRx却假，则称关系R为类k中非对称的关系（非对称关系）。例如，两条直线之间的平行关系、垂直关系、 两个数之间的相等关系等都是对称的关系；两个实数之间的大于关系、 小于关系等部是反对称的关系，两个实数之间的不大于关系， 不小于关系等则是非对称的关系， 这是因为由a不大于b， 并不能断定b是否不大于a。2

对称性关系推理对称性关系推理是指前提和结论都是具有对称性的关系判断的推理。 所谓对称性关系是指：当，且仅当对象a和b之间有一定关系时， 对象b和a之间也有这种关系。如，等于关系、某些亲属关系、同一关系、 同时关系，同地关系，全异关系等都属于对称性关系。 根据这些对称性关系进行推演的关系推理都是对称性关系推理。例如，数学里的“a=b， 所以，b=a，”就属于具有等于性的对称性关系推理。如，“a是b的兄弟，所以，b也是a的兄弟。”这就是表示某些亲属关系的对称性的关系推理。 又如，“李白和杜甫是同时代的人，所以， 杜甫和李白是同时代的人。”这是表示同时关系的对称性关系推理。

对称性关系推理可以用如下的公式来表示：R(a，b)→R(b，a)。或者是：aRb，所以， bRa。在这里，R代表对称性关系，a和b分别为两类对象。 对称性关系推理的规则：如果判断R(a，b)真，那么，R(b，a)也真。2

关系判断关系判断的定义关系判断是断定对象与对象之间关系的简单判断。简单判断除了性质判断以外，还有关系判断，关系判断是断定对象与对象之间关系的判断。

例如:①长江长于黄河；②郑州在洛阳与开封之间；③笑比哭好；④徐特立与毛泽东有师生关系。这四个判断都是关系判断。例①断定了“长江”与“黄河”之间有“长于”的关系；例②断定了“郑州”和“洛阳”、“开封”三者之间存在前者在后面二者之间的“在...之间”的关系；例③断定了“笑”与“哭”之间有“比....好”的关系；例④判定了“徐特立”与“毛泽东”之间有“师生关系”。

关系判断和性质判断不同。性质判断是断定对象是否具有某种性质(即对象与性质之间的关系) 的判断，主项只有一个; 而关系判断却是断定对象与对象之间是否具有某种关系的判断，而关系总是存在于两个或两个以上的对象之间，因此，关系判断的对象就有两个或两个以上，即主项至少是两个。存在于两个对象之间的关系叫两项关系，存在于三个对象之间的关系叫三项关系，存在于三个以上对象之间的关系叫多项关系3。

关系判断的组成关系判断由三部分组成：关系者项、关系项、量项。

关系者项。反映一定关系承担者的概念(或表示一定关系所联结的概念)，也就是关系判断的主项。如前述各例中的“长江"、“黄河’，、“郑州"、“开封"、“笑’’、“哭"、“徐特立"、“毛泽东’’。在关系判断中，关系者项至少有两个，也可以是三个或多个。在两项关系中，在前的关系者项叫关系者前项，在后的关系者项叫关系者后项。若有三个以上关系者项，则按先后次序可分别称之为第一、第二、第三……关系者项。通常用“a"、“b’’、****“c”……表示。

关系项。表示各关系者项之间的关系的概念，也就是关系判断的谓项。上述各例中的“长于"、“比……好”、“师生关系"、“在……之间”都是关系项，通常用“R"表示。

量项(关系量项)。表示关系者项数量的概念。每一个关系者项都可以有量项。如“有的美国人高于所有中国入"。其中，“有的”“所有"都是关系者项的量项3。

关系判断的结构式根据上述关系判断的组成要素，我们就可以把具有两项关系的判断的结构式表示为；所有(有的)aR有的(所有)b。具体表达为四种基本形式。

所有aR所有b；

所有aR有的b；

有的aR所有b；

有的aR有的b。

实际上，关系判断既有肯定形式，又有否定形式。例如“5大于3"是肯定关系判断。而“3不大于5”，就是否定关系判断。它否定了“3”对于“5’’具有“大于"的关系。这样，两项关系判断的基本形式应该还有另外几种。

所有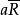 所有b；

所有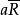 有的b；

有的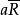 有的b；

有的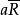 所有b。

**在关系判断中，如果关系者项表示的是一个或一类对象，量项可以省略。**这样，二项关系判断可以写为：

R(a、b)或aRb；

一个三项的关系判断可写为：

R(a、b，c)；3

关系的分类对象间的关系多种多样，因而关系判断中的关系也有多种多样。关系判断的逻辑性质取决子关系的性质。常见的有两种性质的关系：对称性关系（对称关系、反对称关系、非对称关系）；传递性关系（传递关系；反传递关系；非传递关系）。3