[科普中国]-割圆曲线

定义

割圆曲线是一种平面曲线，其直角坐标方程为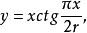其中r 为以原点为圆心的圆的半径(图1，r=OA)2。

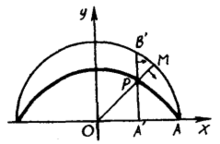
割圆曲线亦可用动点的轨迹来定义。直线OM绕点O匀速转动(顺时针方向)，与y轴平行的直线A'B'同时开始沿x轴方向平移。当OM旋转90°时，A'B'恰好平移距离OA=r，这样，OM与A'B'的交点P的轨迹就是割圆曲线之一段2。

割圆曲线是在研究解古代三大作图问题(化圆为方、三等分角和倍立方)时的一种数学成果。大约在公元前420年，希庇亚斯发现了称做割圆曲线(quadratrix)的超越曲线，并发现它可以用于解三等分角和化圆为方两个问题3。

割圆曲线的形成割圆曲线可由以下方法形成——

作一个正方形，它的底边为AB，让AB从底边的位置开始沿反时针方向，以一个固定的角速度绕A点旋转，另一方面，平行于AB的线段(其端点位于AD和BC)也从AB开始，以一个固定的线速度运动。这两条运动线段的交点所形成的便是割圆****曲线。以下的比总是相等的：

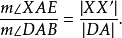
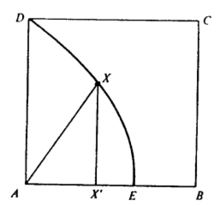
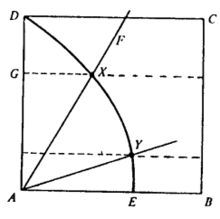
图4说明了与割圆曲线上D，K和E相联系的一些点。水平的虚线段表示边以固定的线速度运动，而沿圆弧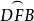所引的半径表示线段以固定的角速度运动。它们的交点D，I，J，K，L，M，E是割圆曲线上的点4。

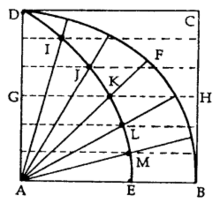
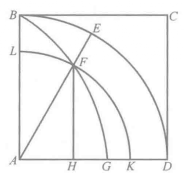
化圆为方—求圆面积问题设ABCD 是正方形，BED 是圆的一个象限，圆心在点A。

设：(1)圆的半径均匀地绕着A转动，由AB转到AD的位置；(2)同时，直线BC亦均匀地沿着BA与AD平行地移动，最后移到AD的位置。于是转动的半径和移动的直线最后都与AD重合，而在这以前，转动的半径和移动的直线将有交点，如F或N。这种点的轨迹称为割圆曲线(quadratrix)，图5。

这曲线的性质是： ∠BAD :∠EAD= 弧BED :弧ED= AB :FH。

设割圆曲线与AD 交于G，如果能够证明：

象限BED的弧长：AB= AB：AG。

那么就可求得象限BED的弧长，因而就可求得圆周的长度。设上述的比不等于AB：AG，不妨设这比等于AB：AK，AK或大于AG，或小于AG。

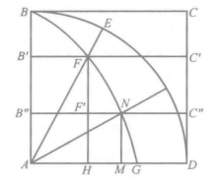
(1) 设AK>AG，图6，以A 为圆心,AK 为半径,作象限KFL 交割圆曲线于F，交AB于L。联结AF，延长AF交圆周BED于E，作FH 垂直于AD。

根据假定

弧BED :AB= AB : AK= 弧BED : 弧LFK。

所以，AB= 弧LFK，

但由割圆曲线的性质：

AB : FH=弧BED :弧ED=弧LFK:弧FK。

已经证得AB=弧LFK，则得FH=弧FK，这是不可能的，因此AK 不能大于AG。

(2) 设AK