基本介绍
对于区间估计问题,贝叶斯方法具有处理方便和含义清晰的优点,而经典方法寻求的置信区间常受到批评。当参数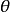 的后验分布
的后验分布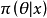 获得以后,立即可计算
获得以后,立即可计算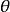 落在某区间[a,b] 内的后验概率,譬如
落在某区间[a,b] 内的后验概率,譬如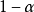 ,即
,即
 反之,若给定概率
反之,若给定概率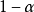 ,要找一个区间[a,b] 使上式成立,这样求得的区间就是贝叶斯区****间估计,又称为可信区间,这是在
,要找一个区间[a,b] 使上式成立,这样求得的区间就是贝叶斯区****间估计,又称为可信区间,这是在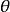 为连续型随机变量场合,若
为连续型随机变量场合,若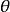 为离散型随机变量,对给定的概率
为离散型随机变量,对给定的概率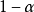 ,满足上式的区间[a,b] 不一定存在,这时只有略微放大上式左端概率,才能找到a 与b,使得
,满足上式的区间[a,b] 不一定存在,这时只有略微放大上式左端概率,才能找到a 与b,使得
 这样的区间也是
这样的区间也是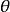 的贝叶斯可信区间。它的一般定义如下:
的贝叶斯可信区间。它的一般定义如下:
设参数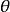 的后验分布为
的后验分布为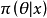 ,对给定的样本观测值x和概率
,对给定的样本观测值x和概率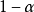
 若存在这样的两个统计量
若存在这样的两个统计量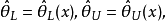 使得
使得
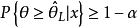 则称区间
则称区间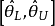 为参数
为参数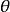 的可信水平为
的可信水平为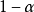 贝叶斯可信区间,或简称为
贝叶斯可信区间,或简称为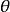 的
的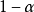 可信区间。而满足
可信区间。而满足
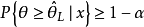
的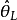 称为
称为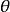 的
的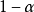 (单侧)可信下限。满足
(单侧)可信下限。满足
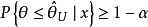 的
的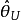 称为
称为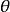 的
的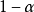 (单侧)可信上限。
(单侧)可信上限。
这里的可信水平和可信区间与经典统计中的置信水平与置信区间虽是同类的概念,但两者还有本质差别,主要表现在如下两点:
1.在条件方法下,对给定的样本观测值x和可信水平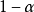 ,通过后验分布可求得具体的可信区间,譬如,
,通过后验分布可求得具体的可信区间,譬如,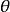 的可信水平为0.9的可信区间是[1.5,2.6],这时我们可以写出
的可信水平为0.9的可信区间是[1.5,2.6],这时我们可以写出
 还可以说:“
还可以说:“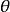 属于这个区间的概率是0.9”或“
属于这个区间的概率是0.9”或“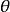 落入这个区间的概率是0.9”,可对置信区间就不能这么说,因为经典统计认为
落入这个区间的概率是0.9”,可对置信区间就不能这么说,因为经典统计认为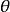 是常量,它要么在[1.5,2.6]内,要么在此区间之外。此时
是常量,它要么在[1.5,2.6]内,要么在此区间之外。此时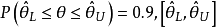 为一随机区间,而[1.5,2.6]为此随机区间的一个观察值,其频率解释为:在大量这种观察中,得到大量的确定区间,大约有90%的区间包含参数真值
为一随机区间,而[1.5,2.6]为此随机区间的一个观察值,其频率解释为:在大量这种观察中,得到大量的确定区间,大约有90%的区间包含参数真值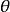 。
。
2.在经典统计中寻求置信区间有时是困难的,因为它要设法构造一个枢轴量,使它的分布不含有未知参数,这是一项技术性很强的工作,不熟悉“抽样分布”是很难完成的,可寻求可信区间只要利用后验分布,不需要再去寻求另外的分布,两种方法相比,可信区间的寻求要简单得多。
最大后验密度可信区间等尾可信区间在实际中常被使用,但不是最理想的,最理想的可信区间应是区间长度最短,这只要把具有最大后验密度的点都包含在区间内,而在区间外的点上的后验密度函数值不超过区间内的后验密度函数值,这样的区间称为最大后验密度( Highest Posterior Density,简称HPD)可信区间,它的一般定义如下:
设参数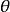 的后验密度为
的后验密度为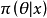 ,对给定的概率
,对给定的概率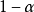
 若存在区间
若存在区间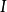 ,满足下列条件:
,满足下列条件:
(1) 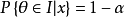 ;
;
(2)对任给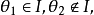 总有
总有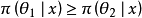 。
。
则称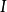 为
为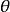 的可信水平为
的可信水平为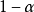 的最大后验密度(HPD)可信区间,简称(
的最大后验密度(HPD)可信区间,简称(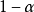 )HPD可信区间。这个定义仅对后验密度函数而给的,这是因为当
)HPD可信区间。这个定义仅对后验密度函数而给的,这是因为当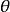 为离散型随机变量时,HPD可信区间很难实现1。
为离散型随机变量时,HPD可信区间很难实现1。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国