[科普中国]-指数平滑预测法

基本内容

时间序列是指同一变量按事件发生的先后顺序排列起来的一组观察值或记录值。构成时间序列的要素有两个：其一是时间，其二是与时间相对应的变量水平。 实际数据的时间序列能够展示研究对象在一定时期内的发展变化趋势与规律，因而可以从时间序列中找出变量变化的特征、趋势以及发展规律，从而对变量的未来变化进行有效地预测。

时间序列预测法的基本特点是1：假定事物的过去趋势会延伸到未来；预测所依据的数据具有不规则性；撇开了市场发展之间的因果关系。

时间序列预测的主要方法：平均（平滑）预测法、长期趋势预测法、季节变动预测法、指数平滑预测法。

**产生背景：**指数平滑由布朗提出，他认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续的未来，所以将较大的权数放在最近的态势。

**基本原理：**指数平滑法是移动平均法中的一种，其特点在于给过去的观测值不一样的权重，即较近期观测值的权数比较远期观测值的权数要大。根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。

分类据平滑次数的不同，指数平滑预测法可以分为：一次指数平滑预测法、二次指数平滑预测法、高次指数平滑预测法1。

一次指数平滑预测法当时间数列无明显的趋势变化，可用一次指数平滑预测。其预测公式为： 。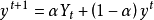

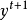--t+1期的预测值，即本期（t期）的平滑值St ；
yt--t期的实际值；
yt--t期的预测值，即上期的平滑值St-1 。2

指数平滑法初始值的确定

从时间序列的项数来考虑：若时间序列的观察期n大于15时，初始值对预测结果的影响很小，可以方便地以第一期观测值作为初始值；若观察期n小于15，初始值对预测结果影响较大，可以取最初几期的观测值的平均数作为初始值，通常取前3个观测值的平均值作为初始值。

一次指数平滑法的特点
1.调整预测值的能力强。
2.预测值包含的信息量是全部历史数据。
3.加权的特点是离预测期较近的权数较大，较远的权数较小。权数之和为1。

二次指数平滑预测法一次指数平滑法的局限性：一次指数平滑法只适用于水平型历史数据的预测，不适用于呈斜坡型线性趋势历史数据的预测。
解决步骤：
1.先求出一次指数平滑值和二次指数平滑值的差值；
2.将差值加到一次指数平滑值上；
3.再考虑趋势变动值。

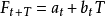
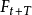为t+T期的预测值；T为t期到预测期的间隔期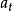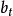数； 、 为参数。

三次指数平滑预测法若时间序列的变动呈现出二次曲线趋势，则需要采用三次指数平滑法进行预测。三次指数平滑是在二次指数平滑的基础上再进行一次平滑，其计算公式为 。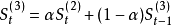

平滑系数的选择在指数平滑法中，预测成功的关键是 的选择3。 的大小规定了在新预测值中新数据和原预测值所占的比例。 值愈大，新数据所占的比重就愈大，原预测值所占比重就愈小，反之亦然。

①当时间序列呈稳定的水平趋势时，α应取较小值，如0.1～0.3；
②当时间序列波动较大，长期趋势变化的幅度较大时，α应取中间值，如0.3～0.5；
③当时间序列具有明显的上升或下降趋势时，α应取较大值，如0.6～0.8；

在实际运用中，可取若干个α值进行试算比较，选择预测误差最小的α值。

优缺点指数平滑预测法的1优点

（1）对不同时间的数据的非等权处理较符合实际情况。
（2）实用中仅需选择一个模型参数，即可进行预测，简便易行。
（3）具有适应性，也就是说预测模型能自动识别数据模式的变化而加以调整。

指数平滑预测法的1缺点

（1）对数据的转折点缺乏鉴别能力，但这一点可通过调查预测法或专家预测法加以弥补。

（2）长期预测的效果较差，故多用于短期预测。

应用举例下期预测数=本期预测数+ 平滑系数（本期实际数- 本期预测数）这个公式的含义是：在本期预测数上加上一部分用平滑系数调整过的本期实际数与本期预测数的差，就可求出下期预测数。一般说来，下期预测数常介乎本期实际数与本期预测数之间。平滑系数的大小，可根据过去的预测数与实际数比较而定。差额大，则平滑系数应取大一些；反之，则取小一些。平滑系数愈大，则近期倾向性变动影响愈大；反之，则近期的倾向性变动影响愈小，愈平滑。这种预测法简便易行，只要具备本期实际数、本期预测数和平滑系数三项资料，就可预测下期数2。例如某种产品销售量的平滑系数为0.4，1996年实际销售量为31万件，预测销售量为33万件。则1997年的预测销售量为：1997年预测销售量= 31万件×0.4+33万件×（1-0.4）=32.2万件。