[科普中国]-光速

简介

光波或电磁波在真空或介质中的传播速度。真空中的光速是目前所发现的自然界物体运动的最大速度。

它与观测者相对于光源的运动速度无关，即相对于光源静止和运动的惯性系中测到的光速是相同的。物体的质量将随着速度的增大而增大，当物体的速度接近光速时，它的质量将趋于无穷大，所以有质量的物体达到光速是不可能的。只有静止质量为零的光子，才始终以光速运动着。光速与任何速度叠加，得到的仍然是光速。速度的合成不遵从经典力学的法则，而遵从相对论的速度合成法则1。

发展历程真空中的光速（speed of light/ velocity of light）是自然界物体运动的最大速度。光速与观测者相对于光源的运动速度无关。物体的质量将随着速度的增大而增大，当物体的速度接近光速时，它的动质量将趋于无穷大，所以质量不为0的物体达到光速是不可能的。只有静质量为零的光子，才始终以光速运动着。光速与任何速度叠加，得到的仍然是光速。真空中的光速是一个重要的物理常量。

真空光速定义值：c0=299792458m/s

光速计算值:c0=299792.458km/s (一般取300000km/s）作用：当某物体运动速度相对于另一物体接近光速，某物体的时间相对于另一物体减慢，时间变化符合洛伦兹变换。（二十世纪七十年代通过卫星和地面天文台观测日食的同一时间位置的不同得以证实）光速是目前已知的最大速度，物体达到光速时动能无穷大，所以按当前人类的认知来说达到光速不可能，所以光速、超光速的问题不在物理学讨论范围之内。

自20世纪初起，我们的理论一直受制于爱因斯坦验证的光速极限，即每秒186282英里(约合每秒30万公里)。即使我们把宇宙飞船加速到这一速度，到达距离我们最近的恒星系统半人马座阿尔法星(距离我们大约4.3光年)并返回，也需要近十年时间。此外，宇宙飞船本身还要考虑能量限制。因此，必须要实现突破光速极限才有可能实现这些目的。科学家们实施了许多相关的实验，比如由美国普林斯顿大学科学家王利军(Lijun Wang)于2000年进行的实验和德国科学家于2007年进行的实验都取得了一定的进展。最初，科学家们坚信没有任何物质或信息能够突破光速，但光脉冲却能够做到。在真空状态下，在不同位置测到的光脉冲似乎以一种难以置信的速度在传播。不过，这一速度仍然无法对我们太空旅行提供太大的帮助。2007年的实验仍然存在争议。

贝勒大学物理学教授杰拉德-克利弗尔认为，在“量子纠缠”现象中，信息的传播速度似乎比光速快。2007年和2008年的两次实验表明，“量子纠缠”的速度至少是光速的1万倍。未来实现超光速的方法可能是跳跃到多维空间中。美国宇航局突破推进物理学计划前负责人马克-米利斯现致力于研究星际旅行，他表示，“肯定还有我们没发现的物理学领域。”米利斯举例指出，暗物质和暗能量或许能够为我们带来曙光。

真空中的光速等于299,792,458米/秒（1,079,252,848.88千米/小时）。[2]这个速度并不是一个测量值，而是一个定义。它的计算值为（299792500±100）米/秒。国际单位制的基本单位米于1983年10月21日起被定义为光在1/299,792,458秒内传播的距离。使用英制单位，光速约为186,282.397英里/秒，或者670,616,629.384英里/小时，约为1英尺/纳秒。

在任何透明或者半透明的介质（比如玻璃和水）中，光速会降低；光在真空中的速度和光在某种介质中的速度之比就是这种介质的折射率。重力的改变能够弯曲光所传播的空间，使光像通过凸透镜一样发生弯曲，看上去绕过了质量较大的天体。光弯曲的现象叫做引力透镜效应，根据变化了的光线在光谱外波段呈现的不规则程度，可以推算发光星系的年龄和距离。

2011年9月22日，意大利物理学家在OPERA实验中发现了一种超出光速40322.58分之一的中微子，如果实验数据确凿无误，爱因斯坦的相对论将会受到挑战。但是随后便发现，该实验结果为设备线路接错而造成。该实验结果于2012年6月8日被该小组宣布撤销.根据爱因斯坦的相对论，没有任何物体或信息运动的速度可以超过真空中的光速(c)。

介质影响令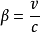 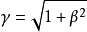， 且设v是静止介质中的光速，u是介质的运动速度，v'是所要求得的运动介质中的光速。另请不要在意下文矢量的书写

光在不同介质中的速度不同，由于光是电磁波，因此光速也就依赖于介质的介电常数和磁导率。在各向同性的静止介质中，光速是一个小于真空光速c的定值。如果介质以一定的速度运动，则一般求光速的方法是先建立一个随动参考系，其中的光速是静止介质中的光速，然后通过参考系变换得到运动介质中的光速；或者可以直接用相对论速度叠加公式去求运动介质中的光速。

光和声虽然都具有波动性质，但两者波速的算法是完全不同的。以声音实验为例：空气对地面静止，第1次我们不动测得我们发出的声音1秒钟前进了300米；第二次我们1秒钟匀速后退1米，测得声音距我们301米，得到结论：两次声音相对地面速度不变，相对我们，第一次300米/秒；第2次301米/秒。在牵涉到的速度远小于光速的情况下，声速满足线性叠加。

换做光实验，我们用玻璃介质再做一次，静止玻璃中的光速，在各个方向上都是相等的。我们再做一个我们不动，让玻璃匀速运动的实验，会发现光对玻璃的速度在不同方向上是不等的，但不是简简单单的线性叠加了，而是遵循相对论速度叠加：

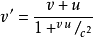其实在前述声速实验中，声速严格来讲遵循的也是相对论速度叠加，只是若u、v都远小于光速c，则式子中 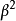是个很小的值，近似略去之后就得v'≈v+u，回到经典的线性叠加形式。

所以，千万不可以用低速条件下机械波的近似规律去硬套光波。作为狭义相对论基本假设之一的光速不变原理，永远指的是真空中的光速c不变，它是基本物理常数之一。如果有介质，就需要利用相对论速度叠加公式去求光速，切忌用简单线性叠加。对光速不变原理的正确理解，是正确理解狭义相对论的关键之一。

不同介质中有不同的光速值。1850年菲佐用齿轮法测定了光在水中的速度，证明水中光速小于空气中的光速。几乎在同时，傅科用旋转镜法也测量了水中的光速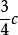（ ），得到了同样结论。这一实验结果与波动说相一致而与牛顿的微粒说相矛盾(解释光的折射定律时)，这对光的波动本性的确立在历史上曾起过重要作用。1851年，菲佐用干涉法测量了运动介质中的光速，证实了A.-J.菲涅耳的曳引公式。[玻璃中光速 ]

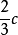光在玻璃中的速度：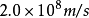

光在酒精中的速度：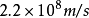

光在水中的速度：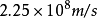

光在冰中的速度：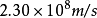

光在真空中的速度：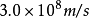

质能方程推导

第一步：要讨论能量随质量变化，先要从量纲得知思路：

能量量纲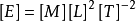 ，即能量量纲等于质量量纲和长度量纲的平方以及时间量纲的负二次方三者乘积。

我们需要把能量对于质量的函数形式化简到最简，那么就要求能量函数中除了质量，最好只有一个其它的变量。

把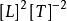 化简，可以得到只有一个量纲-速度量纲[V]的形式：[V]×[V]。

也就是[E]=[M][V]×[V]

可见我们要讨论质能关系，最简单的途径是从速度下手。

第二步：先要考虑能量的变化 与能量的变化有关的有各种能量形式的转化，其中直接和质量有关的只有做功。

那么先来考虑做功对于能量变化的影响。

当外力 作用在静止质量为m0的质点上时，每产生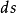 的位移，物体能量增加

。

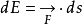考虑最简化的 外力与位移方向相同的情况，上式变成

第三步：怎样把力做功和速度v变化联系起来呢？也就是说怎样来通过力的作用效果来得出速度的变化呢？

我们知道力对物体的冲量等于物体动量的增量。那么，通过动量定理，力和能量就联系起来了：

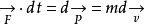
第四步：上式中显然还要参考m质量这个变量，而我们不想让质量的加入把我们力和速度的关系复杂化。我们想找到一种办法约掉m，这样就能得到纯粹的速度和力的关系。

参考 和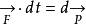 ，我们知道，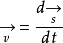

那么可以得到

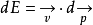
如果考虑最简单的形式：当速度改变和动量改变方向相同：

dE=vdP

第五步：把上式化成能量和质量以及速度三者的关系式（因为我们最初就是要讨论这个形式）：

∵dP=d(mv)，∴dE=vd(mv)

第六步：把上式按照微分乘法分解

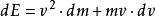
这个式子说明：能量的增量含有质量因速度的增加而增加（量为dm）所产生的能量增量和单纯速度增加产生的能量增量2个部分。（这个观点非常重要，在相对论之前，人们虽然在理论物理推导中认识到质量增加也会产生能量增量，但是都习惯性认为质量不会随运动速度增加而变化，也就是误以为dm恒定为0，这是经典物理学的最大错误之一。）

第七步：我们不知道质量随速度增加产生的增量dm是怎样的，要研究它到底如何随速度增加（也就是质量增量dm和速度增量dv之间的直接关系）：

根据洛仑兹变换推导出的静止质量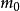 和运动质量m公式：

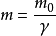
化简成整数次幂形式：

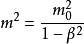
化成没有分母而且m和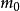 分别处于等号两侧的形式（这样就是得到运动质量m对于速度变化和静止质量的纯粹的函数形式）：

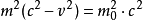
用上式对速度v求导得到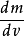 （之所以要这样做，就是要找到质量增量dm和速度增量dv之间最直接的关系，我们这一步的根本目的就是这个）：

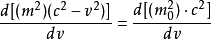(注意式子等号右边是常数的求导，结果为0)

即

即

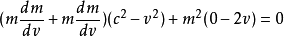
即

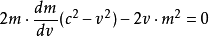
约掉公因式2m(肯定不是0，呵呵，运动质量为0？没听说过)

得到：

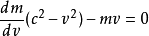
即

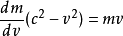
由于dv不等于0（我们研究的就是非静止的情况，运动系速度对于静止系的增量当然不为0）

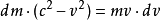
这就是我们最终得到的dm和dv的直接关系

第八步：有了dm的函数，代回到我们第六步的能量增量式

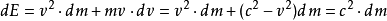
这就是质能关系式的微分形式，它说明：质量的增量与能量的增量成正比，而且比例系数是常数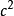

最后一步：推论出物体从静止到运动速度为v的过程中，总的能量增量：

对上一步的结论进行积分，积分区间取质量从静止质量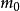 到运动质量m，得到

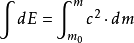
即

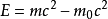
这就是 物体从静止到运动速度为v的过程中，总的能量增量。

其中

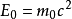称为物体静止时候的静止能量。

称为物体运动时候的总动能（运动总能量）,，此时请注意m为运动状态物体的相对论质量。

总结：对于任何已知运动质量为m的物体，可以用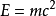 直接计算出它的运动动能。

相关理论在20世纪爱因斯坦狭义相对论中质能等价理论的推论，即著名的方程式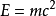 ，式(质能方程)中为E能量，单位电子伏特（eV），m为质量，c为光速；也就是说，一切物质都潜藏着质量乘以光速平方的能量。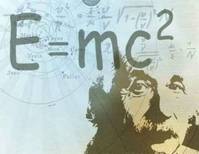一个静止的物体，其全部的能量都包含在静止的质量中。一旦运动，就要产生动能。由于质量和能量等价，运动中所具有的能量应加到质量上，也就是说，运动的物体的质量会增加。当物体的运动速度远低于光速时，增加的质量微乎其微，如速度达到光速的10%时，质量只增加0.5%。但随着速度接近光速，其增加的质量就显著了。如速度达到光速的86.6%时，其质量增加了一倍。这时，物体继续加速就需要更多的能量。当速度趋近光速时，质量随着速度的增加而成几何倍数上升，速度无限接近光速时，质量趋向于无限大，需要无限多的能量。因此，任何物体的运动速度不可能达到光速，只有质量为零（在宇宙大爆发时，即大爆炸初始普朗克时期开端之间有很多能量不为0的粒子的质量为0）的粒子才可以以光速运动，如因科学研究虚构的“光子”、“引力子”这个名称。

真空中的光速是一个物理常数（符号是c），等于299,792,458m/s。

注：光速的方向不恒定。如果在光运行时施加力，那么光的方向进而速度矢量会产生一定的改变。

丹麦天文学家罗默（OleRomer）在17世纪首次成功地计算出光速。他使用木星的一颗卫星有规律的轨道运动作为计时器，每次这颗卫星被巨大的行星（木星）所掩食，他便记录下一个“滴答”。但他发现，从地球上观察，这些滴答的出现并不像预想的那么规律，在一年之中会时而快几分钟，时而慢几分钟。

罗默计算出，这些时延是木星和地球在绕太阳运动时它们之间的距离变化所引起的。通过计算一年里地球、木星及其卫星在轨道上的相对位置，他算出了光穿过宇宙空间的速度。罗默于1676年向法国科学院提交了他的结果，数值与目 前被接受的值之差不超过30%。

对光之本性的理论探讨也使人们对光速有所了解。19世纪60年代中期，苏格兰科学家詹姆斯·克拉克·麦克斯韦创建了一组方程，描述电磁场在空间中的行为。这个方程的一个解表明，电磁波在真空中必须以约为每秒30万公里的速度传播，与罗默及其后人的测量结果相当接近。

伦敦皇家研究院的迈克尔?法拉第用电场和磁场的概念解释静电力和磁场力，并表明光会受到磁场影响。这证实了可见光事实上是电磁波谱中的一部分。对电磁波谱其它部分——微波，红外线，紫外线，X射线和γ射线——传播速度的直接测量表明，它们在真空中都有相同的速度。用于测量光速的实验不断地变得更精确。到20世纪50年代，电子计时装置已经取代了古老的机械设备。20世纪80年代，通过测量激光和频率（f）和波长（λ），运用c=fλ公式计算出了光速（c）。这些计算以米和秒的标准定义为基础，就像现在一样，1米定义为氪-86源产生的光的波长的1,650,763.73倍，1秒则定义为铯-133原子超精细跃迁放出的辐射频率的9,192,631,770倍。这使得c达到非常高的精度，误差只有十亿分之几。

1983年，光速取代了米被选作定义标准，约定为299,792,458m/s，数值与当时的米定义一致。秒和光速的定义值，表示1米从此定义为光在真空中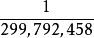 秒内走过的距离。因此自1983年以来，不管我们对光速的测量作了多少精确的修正，都不会影响到光速值，却会影响到米的长度。你有多高事实上是由光速定义的。

但光速还定义着比长度更加基本的东西。阿尔伯特·爱因斯坦的工作表明了光速的真正重要性。由于他的功劳，我们知道，光速不仅仅是光子在真空中运动的速度，还是连接时间与空间的基本常数。

爱因斯坦年轻的时候曾经问自己，如果人运动的速度快到足以跟上光的脚步，光看起来是什么样子的。理论上它看上去像是你身边一个静止的峰，但爱因斯坦知道，麦克斯韦方程组不允许这种结果出现。他得出结论认为，要么是麦克斯韦的理论不适用于运动中的观察者，要么是相对运动力学需要更改。

爱因斯坦在他1905年发表的狭义相对论里解决了这个问题。这一理论基于一个通用原则：相对任何以恒定速度运动的观察者来说，不管这个速度是多少，物理原理及光速都是一样的。爱因斯坦的狭义相对论使我们对时间和空间的观念发生了革命性的变化，强调了光速在物理学中的根本地位。

想象你在一枚火箭里，与一道激光脉冲一同冲入宇宙空间。地球上的观察者会看到这一脉冲以光速远去。无论你相对于地球运动的速度为多少，譬如光速的99%罢，光线仍以光速超越你。看起来似乎很荒谬，但这是真的。使这为真的唯一途径，就是你火箭中的居住者和地球表面的观察者以不同方式衡量时间和空间。

时间与空间看上去当然是不同的，这依赖于你是在地球上还是在宇宙空间里。爱因斯坦的广义相对论将引力描述为时空几何结构的扭曲。这种说法的一个推论，就是始终沿可能的最短路径穿越时空的光线，在大质量物体附近会弯曲。这在1919年日食期间观测掠过太阳附近的星光被太阳的质量所弯曲而得到证明。这一观测使爱因斯坦的理论最终得到接受，并为他赢得了世界性的声誉。

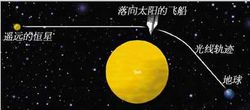但按照基本力学原理，如果光线偏转，它会被加速。这是否将使光速发生变化，动摇相对论的根本原则？在某种意义上是对的：我们从地球上观察到的光速，在它从太阳附近经过时确实会变化。然而相对论和光速不变原理不能被抛弃。

爱因斯坦认识到，引力是无法自由运动的观察者们经历的某种幻象。想象从一堵墙上跳下。在自由落体的过程中，你不会感动周围的引力作用，但任何在地面上瞧着你落下来的人，都会解释说你的运动是引力的作用所致。同样的说法对空间站中的宇航员也适用：他们被提及时总是说成是处在“零重力”环境里，但从地球的表面往上看，我们会用引力吸引来解释他们绕地球的轨道运动。所以当我们从地球上观察时，经过太阳附近的光线看上去弯曲、加速了，但如果我们自由落体地落向太阳，光线看上去会以恒速沿直线经过我们身边。对任何自由落体的观察者来说，经过他的光线都以恒定速度运动。不过，它在掠过扭曲其附近时空的大质量物体时，看上去会弯曲和加速。这表明，引力不能被理解为一个场力，而是应该理解为时空的一种内禀特性。

相对论另一个奇怪的推论是，没有任何物体能加速到光速。不管我们建造动力多么强劲的火箭飞船，它们也永远不能到达光速。这是因为物体运动得越快，其动能越大，惯性也越大。爱因斯坦在他的质能方程中指出，能量和质量或者说惯性相关联。因此一个物体的动能增加，它的惯性也增加，从而越来越难继续加速。这是一个收益递减原理：你对一个物体做的功越多，它就变得越重，加速的效果也越微弱。

把单一电子加速到光速，就需要无限的能量，粒子物理学家们对这一限制深有感触。质子进入美国伊利诺伊州Batawia费米实验室的Tevatron加速器时，它们的速度已经达到光速的99%。加速器的最后阶段使质子的能量提高了100倍，但速度仅增加到光速的99.99995%，与它们进入加速器的速度相比，提高不足1%。

不过，一直与相对论有冲突的量子理论看上去是允许物质以大于光速的速度运动的。在20世纪20年代，量子论显示一个系统相隔遥远的不同组成部分能够瞬时联系。例如，当一个高能光子衰变成两个低能光子时，它们的状态（例如，是顺时针或逆时针自旋）是不定的，直到对它们中间的某一个作出观察才确定下来。另一个粒子看上去感知到它的同伴被进行了一次观测，结果是任何对第二个粒子的测量总会得到与对第一个粒子的测量相一致的结果。这样远距离的瞬时联系，看起来像是一个讯息以无限大的速度在粒子之间传递了。它被爱因斯坦称为“幽灵式的超距作用”，听起来难以置信，但却是真实的现象。

1993年，加利福尼亚大学伯克利分校的RaymondChiao表明，量子理论还允许另一种超光速旅行存在：量子隧穿。想象朝一堵坚实的墙上踢一个足球，牛顿力学预言它会被弹回，但量子力学预言它还有极小的可能出现在墙的另一面。考虑这种情况的一种途径，是想象它能“借”到足够的能量穿越墙壁，并在到达另一面之后立即将能量归还。这并不违反物理定律，因为最终能量、动量和其它属性都得到了保存。德国物理学家维纳·海森堡的测不准原理表明，在一个系统中，总有某些属性——在这一情况中是能量——的值是不能确定的，只能确定在一个区间内，因此量子物理学原理允许系统利用这种不确定性，短时间借到一些额外的能量。在隧穿的情况中，粒子从障碍物的一面消失又从另一面重现的需要几乎可以忽略不计，障碍物可以任意的厚——不过随着厚度增加，粒子隧穿的几率也就迅速地朝零的方向递减，但请注意，不会等于0（如若这样，海森堡原理就会被反对，因为0测值为0是确定的）。

Chiao通过测量可见光光子通过特定过滤器的隧穿时间，证明了隧穿“超光速”的隧穿效应存在。为此，他让这些光子与在相似时间内穿过真空的光子进行比较。结果隧穿光子先到达探测器，Chiao证明它们穿越过滤器的速度可能为光速的1.7倍。

1994年，维也纳技术大学的FerencKraus表明，隧穿时间有一个不依赖于障碍物厚度的上限，这表示光子隧穿障碍物的时间没有上限。德国科隆大学的GunterNimtz也用微波实现了这种“超光速”。他甚至把莫扎特第40号交响曲调制在信号上，以4.7倍光速的速度将它传输通过12厘米厚的障碍物。

研究历史真空中的光速是一个物理常量，国际公认值为c=299792458m/s。17世纪前人们以为光速为无限大，意大利物理学家G.伽利略曾对此提出怀疑，并试图通过实验来检验他设想，在距离很远的两个地方，两人互相用灯光传递信号，最终没能成功。

艾萨克·牛顿也接受光速是有限的观念，在他1704年出版的书《光学》中，他提出光每秒钟可以横越地球16.6次（相当于210,000公里/秒，比正确值低了30%）。这似乎是他自己的推断（不能确知他是否有引用或参考罗默的数据）。

1676年，丹麦天文学家奥劳斯·罗默（1644~1710）利用木星卫星的星蚀时间变化证实光是以有限速度传播的。他利用木星的木卫一在木星在木星圆面上的投影作周期性变化的现象，第一次定量的估计出光速。艾欧的公转轨道可以用来计算时间，因为它会规律的进入木星的阴影中一段时间。罗默观测到当地球在最接近木星时，艾欧的公转周期是42.5小时，当地球远离木星时，艾欧从阴影中出现的时间会比预测的越来越晚，很明显的是因为木星与地球的距离增加，使得"信号"要花更多的时间传递。光要通过行星之间增加的距离，使得计时的信号在第一次和下一次之间因而延长了额外的时间。当地球向木星接近时，情形则正好相反。罗默观测到艾欧在接近的40 个轨道周期中周期比远离的40个轨道周期缩短了22分钟。以这些观测为基础，罗默认为在80个轨道周期中光线要多花费22分钟行走艾欧与地球之间增加的距离。这意味着地球经历了80个艾欧轨道周期（42.5小时）的时间，光线只要花22分钟。这对应于一个地球在轨道上绕着太阳运动和光速之间的一个比例。意味着光速是地球的轨道速度的9,300倍，与现 在的数值10,100倍比较，相差较小。但是因为这种观测是很困难的，因而日后被其他的方法所取代。

在当时，天文单位的估计数值是大约1亿4千万公里。克里斯蒂安·惠更斯结合了天文单位和罗默的时间估计，每分钟的光速是地球直径的1,000倍，他似乎误解了罗默22分钟的意思，以为是横越地球轨道所花费的时间。这相当于每秒220,000公里（136,000英里），比现 在采用的数值低了26%，但仍比当时使用其他已知的物理方法测得的数值为佳。

即使如此，靠著这些观测，光速是有限的仍不能被大众满意的接受（著名的有吉恩·多米尼克·卡西尼），直到在詹姆斯·布雷德里（1728）的观测之后，光速是无限的想法才被扬弃。布雷德里推论若光速是有限的，则因为地球的轨道速度，会使抵达地球的星光有一个微小角度的偏折，这就是所谓的光行差，他的大小只有1/200度。布雷德里计算的光速为298,000公里/秒（185,000英里/秒），这与现 在的数值只有不到1%的差异。光行差的效应在19世纪已经被充分的研究，最著名的学者是瓦西里·雅可夫列维奇·斯特鲁维。

1849年，法国物理学家A.H.L.菲佐用旋转齿轮法首次在地面实验室中成功地进行了光速测量，最早的结果为c=315000千米/秒。1862年，法国实验物理学家J.-B.-L.傅科根据D.F.J.阿拉戈的设想用旋转镜法测得光速为c=(298000±500)千米/秒。19世纪中叶J.C.麦克斯韦建立了电磁场理论，他根据电磁波动方程曾指出，电磁波在真空中的传播速度等于静电单位电量与电磁单位电量的比值，只要在实验上分别用这两种单位测量同一电量(或电流)，就可算出电磁波的波速。1856年，R.科尔劳施和W.韦伯完成了有关测量，麦克斯韦根据他们的数据计算出电磁波在真空中的波速值为3.1074×10^5千米/秒，此值与菲佐的结果十分接近，这对人们确认光是电磁波起过很大作用。

1926年，美国物理学家A.A.迈克耳孙改进了傅科的实验，测得c=(299796±4)千米/秒，他于1929年在真空中重做了此实验，测得c=299774千米/秒。后来有人用光开关(克尔盒)代替齿轮转动以改进菲佐的实验，其精度比旋转镜法提高了两个数量级。1952年，英国实验物理学家K.D.费罗姆用微波干涉仪法测量光速得c=(299792.50±0.10)千米/秒。此值于1957年被推荐为国际推荐值使用，直至1973年。

1972年，美国的K.M.埃文森等人直接测量激光频率ν和真空中的波长λ，按公式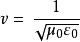 （其中v为真空中电磁波的速度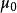， 为真空磁导率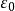， 为真空介电常数）算得c=(299792458±1.2)米/秒。1975年第15届国际计量大会确认上述光速值作为国际推荐值使用。1983年17届国际计量大会通过了米的新定义，在这定义中光速c=299792458米/秒为规定值，而长度单位米由这个规定值定义。既然真空中的光速已成为定义值，以后就不需对光速进行任何测量了。

1983年，光速取代了保存在巴黎国际计量局的由90%铂和10%铱的合金制成的米原器被选作定义“米”的标准，并且约定光速严格等于299,792,458m/s，此数值与当时的米的定义和秒的定义一致。后来，随着实验精度的不断提高，光速的数值有所改变，米被定义为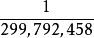 秒内真空中光通过的路程。

1849年，菲索用旋转齿轮法求得 。他是第一位用实验方法，测定地面光速的实验者。 实验方法大致如下：光从半镀银面反射后，经高速旋转的齿轮投向反射镜，再沿原路返回。如果齿轮转过一齿所需的时间，正好与光往返的时间相等，就可透过半镀银面观测到光，从而根据齿轮的转速计算出光速。

1862年，法国的傅科用旋转镜法测空气中的光速，原理和斐索的旋转齿轮法大同小异，他的结果是 。

第三位在地面上测到光速的是考尔纽。1874年他改进了菲索的旋转齿轮法，得 。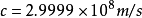

阿尔伯特·迈克耳孙改进了傅科的旋转镜法，多次测量光速。1879年，得 c = (2.99910±0.00050) ×10^8m/s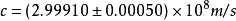 ；1882年得 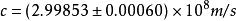。后来，他综合旋转镜法和旋转齿轮法的特点，发展了旋转棱镜法，1924～1927年间，得 。

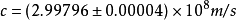迈克耳逊在推算真空中的光速时，应该用空气的群速折射率，可是他用的却是空气的相速折射率。这一错误在1929年被经改正后，1926年的结果应为 。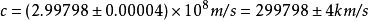

后来，由于电子学的发展，用克尔盒、谐振腔、光电测距仪等方法，光速的测定，比直接用光学方法又提高了一个数量级。

60年代雷射器发明，运用稳频雷射器，可以大大降低光速测量的不确定度。

1973年达0.004 ppm，终于在1983年第十七届国际计量大会上作出决定，将真空中的光速定为精确值。

近代测量真空中光速实验的简表：

|| ||

（注：esu即electrostatic units的缩写；emu为electromagnetic units的缩写。）

研究方法天文学方法1676年，丹麦天文学家O.C.罗默利用木星卫星的星蚀时间变化证实光是以有限速度传播的。1727年，英国天文学家J.布拉得雷利用恒星光行差现象估算出光速值为c=303000千米/秒。

罗默的卫星蚀法

光速的测量，首先在天文学上获得成功，这是因为宇宙广阔的空间提供了测量光速所需要的足够大的距离．早在1676年丹麦天文学家罗默（1644—1710）首先测量了光速．由于任何周期性的变化过程都可当作时钟，他成功地找到了离观察者非常遥远而相当准确的“时钟”，罗默在观察时所用的是木星每隔一定周期所出现的一次卫星蚀．他在观察时注意到：连续两次卫星蚀相隔的时间，当地球背离木星运动时，要比地球迎向木星运动时要长一些，他用光的传播速度是有限的来解释这个现象．光从木星发出（实际上是木星的卫星发出），当地球离开木星运动时，光必须追上地球，因而从地面上观察木星的两次卫星蚀相隔的时间，要比实际相隔的时间长一些；当地球迎向木星运动时，这个时间就短一些．因为卫星绕木星的周期不大（约为1.75天），所以上述时间差数，在最合适的时间不致超过15秒（地球的公转轨道速度约为30千米/秒）．因此，为了取得可靠的结果，当时的观察曾在整年中连续地进行．罗默通过观察从卫星蚀的时间变化和地球轨道直径求出了光速．由于当时只知道地球轨道半径的近似值，故求出的光速只有214300km/s．这个光速值尽管离光速的准确值相差甚远，但它却是测定光速历史上的第一个记录．后来人们用照相方法测量木星卫星蚀的时间，并在地球轨道半径测量准确度提高后，用罗默法求得的光速为299840±60km/s．

布莱德雷的光行差法

1728年，英国天文学家布莱德雷（1693—1762）采用恒星的光行差法，再一次得出光速是一有限的物理量．布莱德雷在地球上观察恒星时，发现恒星的视位置在不断地变化，在一年之内，所有恒星似乎都在天顶上绕着半长轴相等的椭圆运行了一周．他认为这种现象的产生是由于恒星发出的光传到地面时需要一定的时间，而在此时间内，地球已因公转而发生了位置的变化．他由此测得光速为：C=299930千米/秒

这一数值与实际值比较接近．

以上仅是利用天文学的现象和观察数值对光速的测定，而在实验室内限于当时的条件，测定光速尚不能实现．

地面测量方法光速的测定包含着对光所通过的距离和所需时间的量度，由于光速很大，所以必须测量一个很长的距离和一个很短的时间，大地测量法就是围绕着如何准确测定距离和时间而设计的各种方法．

最早于1629年艾萨克·毕克曼（Beeckman）提出一项试验，一人将遵守闪光灯一炮反映过一面镜子，约一英里。伽利略认为光速是有限的，1638年他请二个人提灯笼各爬上相距仅约一公里的山上，第一组人掀开灯笼，并开始计时，对面山上的人看见亮光后掀开灯笼，第一组看见亮光后，停止计时，这是史上著名的测量光速的掩灯方案，这种测量方法实际测到的主要只是实验者的反应和人手的动作时间。

伽利略测定光速的方法

物理学发展史上，最早提出测量光速的是意大利物理学家伽利略．1607年在他的实验中，让相距甚远的两个观察者，各执一盏能遮闭的灯，如图所示：观察者A打开灯光，经过一定时间后，光到达观察者B，B立即打开自己的灯光，过了某一时间后，此信号回到A，于是A可以记下从他自己开灯的一瞬间，到信号从B返回到A的一瞬间所经过的时间间隔t．若两观察者的距离为S，则光的速度为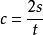

因为光速很大，加之观察者还要有一定的反应时间，所以伽利略的尝试没有成功．如果用反射镜来代替B，那么情况有所改善，这样就可以避免观察者所引入的误差．这种测量原理长远地保留在后来的一切测定光速的实验方法之中．甚至在现代测定光速的实验中仍然采用．但在信号接收上和时间测量上，要采用可靠的方法．使用这些方法甚至能在不太长的距离上测定光速，并达到足够高的精确度．

旋转齿轮法

用实验方法测定光速首先是在1849年由斐索实验．他用定期遮断光线的方法（旋转齿轮法）进行自动记录．实验示意图如下．从光源s发出的光经会聚透镜L1射到半镀银的镜面A，由此反射后在齿轮W的齿a和a’之间的空隙内会聚，再经透镜L2和L3而达到反射镜M，然后再反射回来．又通过半镀镜A由L4集聚后射入观察者的眼睛E．如使齿轮转动，那么在光达到M镜后再反射回来时所经过的时间△t内，齿轮将转过一个角度．如果这时a与a’之间的空隙为齿a（或a’）所占据，则反射回来的光将被遮断，因而观察者将看不到光．但如齿轮转到这样一个角度，使由M镜反射回来的光从另一齿间空隙通过，那么观察者会重新看到光，当齿轮转动得更快，反射光又被另一个齿遮断时，光又消失．这样，当齿轮转速由零而逐渐加快时，在E处将看到闪光．由齿轮转速v、齿数n与齿轮和M的间距L可推得光速c=4nvL．

在斐索所做的实验中，当具有720齿的齿轮，一秒钟内转动12.67次时，光将首次被挡住而消失，空隙与轮齿交替所需时间为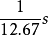

在这一时间内，光所经过的光程为2×8633米，所以光速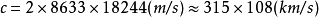

在对信号的发出和返回接收时刻能作自动记录的遮断法除旋转齿轮法外，在现代还采用克尔盒法．1941年安德孙用克尔盒法测得：c=299776±6km/s，1951年贝格斯格兰又用克尔盒法测得c=299793.1±0.3km/s．

旋转镜法

旋转镜法的主要特点是能对信号的传播时间作精确测量．1851年傅科成功地运用此法测定了光速．旋转镜法的原理早在1834年1838年就已为惠更斯和阿拉果提出过，它主要用一个高速均匀转动的镜面来代替齿轮装置．由于光源较强，而且聚焦得较好．因此能极其精密地测量很短的时间间隔．实验装置如图所示．从光源s所发出的光通过半镀银的镜面M1后，经过透镜L射在绕O轴旋转的平面反射镜M2上O轴与图面垂直．光从M2反射而会聚到凹面反射镜M3上，M3的曲率中心恰在O轴上，所以光线由M3对称地反射，并在s′点产生光源的像．当M2的转速足够快时，像S′的位置将改变到s〃，相对于可视M2为不转时的位置移动了△s的距离可以推导出光速值。式中w为M2转动的角速度．l0为M2到M3的间距，l为透镜L到光源S的间距，△s为s的像移动的距离．因此直接测量w、l、l0、△s，便可求得光速。

在傅科的实验中：L=4米，L0=20米，△s=0.0007米，W=800×2π弧度/秒，他求得光速值c=298000±500km/s．

另外，傅科还利用这个实验的基本原理，首次测出了光在介质（水）中的速度v