平凸透镜和双凸透镜的区别
双凸透镜,两面入射的光,折射率相同。焦距也一样。
平凸透镜,两面入射的光,折射率稍有差别。所以实际上两边的焦距也有所不同。使用时,不能颠倒。
作用这类透镜用于汇聚平行光,或把点光源转化成平行光。
合理选择材料(纹理,气泡,杂质,均匀性);在研磨时,考虑到了用于可干涉光时,不产生散乱(划伤,凹痕,光泽)。
规格品有没镀膜和镀了可见光带域的防反射多层膜透镜。
望远镜:
1609年5月,著名科学家伽利略45岁的时候访问了威尼斯。在那里他听到了荷兰人造出望远镜的故事,并为此兴奋不已。
伽利略马上动手制造自己的望远镜。他在一根铅管两端,装上一片平凸透镜和一片平凹透镜。平凹透镜靠近眼的一端,称为目镜。平凸透镜靠近观测物一端,称为物镜。他用自制的望远镜观测物体时,远处的物体被放大了许多倍。
伽利略虽然不是第一个发明望远镜的人,但以他科学家的敏感,成为第一个将望远镜对准星空的人。从此,天文望远镜诞生了,天文学获得了探索宇宙的新武器,并由此取得了一个又一个惊人的发现。1
平凸透镜的焦距计算举例有一定厚度平凸透镜的焦距公式计算
例如:厚度为5,半径为20的平凸透镜的焦距
(1) 如果是凸透镜平面的圆半径:
1。计算凸透镜的球半径:r^2=20^2+(r-5)^2,r=42.5;
2。做平行于光轴的直线AA',交凸透镜球面于点A,直线AA"垂直于光轴,与光轴的交点为A",直线段AA"的长度是h,做直线OA、FA,其中O是球心,F是焦点,过点A做凸透镜球面的切线AB,交光轴于点B,则OA垂直AB,直线OA就是入射光线AA'的法线;
3。计算入射角的正弦值:因为AA'平行光轴OF,因此入射角a=∠AOB,Sin(a)=Sin(AOB)=h/r,∠AOB=ArcSin(h/r);
4。设凸透镜所用材料的折射率为n,则出射角的正弦值 Sin(b)=Sin(a)/n=(h/r)/n=(h*n)/r,即Sin(OAF)=(h*n)/r,∠OAF=ArcSin[(h*n)/r];
5。∠AFO=∠AOB-∠OAF=ArcSin[(h*n)/r]-ArcSin(h/r),tg(AFO)=tg{ArcSin[(h*n)/r]-ArcSin(h/r)}=AA"/FA"=h/FA",FA"=h/tg{ArcSin[(h*n)/r]-ArcSin(h/r)};
6。一面是平面的薄凸透镜,光心可以近似的认为是平面的圆心,因此焦距f=OF+(r-5)=(FA"-OA")+(r-5),而OA^2=OA"^2+AA"^2,即OA"=√(OA^2-AA"^2)=√(r^2-h^2);
7。最后,把FA"、OA"代入,化简计算就可以算出焦距f了。
(2)如果是凸透镜的球半径,则以上步骤中的第一步可以省略,直接从第二步开始算起就行了。
用牛顿环仪测平凸透镜的曲率半径牛顿环仪是由待测平凸透镜(凸面曲率半径约为200~700cm)和磨光的平玻璃板叠合装在金属框架中构成,当一曲率半径很大的平凸透镜的凸面与一磨光平玻璃板相接触时,在透镜的凸面与平玻璃板之间将形成一空气薄膜,离接触点等距离的地方,厚度相同。若以波长为λ的单色平行光投射到这种装置上,则由空气膜上下表面反射的光波将互相干涉,形成的干涉条纹为膜的等厚各点的轨迹,这种干涉是一种等厚干涉。
在反射方向观察时,将看到一组以接触点为中心的亮暗相间的圆环形干涉条纹,而且中心是一暗斑,如果在透镜方向观察,则看到的干涉环纹与反射光的干涉环纹的光强分布恰成互补,中心是亮斑,原来的亮环处变为暗环,暗环处变为亮环,这种干涉现象最早为牛顿所发现,故称牛顿环。
原理1、 牛顿环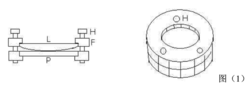
牛顿环仪是由待测平凸透镜(凸面曲率半径约为200~700cm)L和磨光的平玻璃板P叠合装在金属框架F中构成图1。框架边上有三个螺旋H,用以调节L和P之间的接触,以改变干涉环纹的形状和位置。调节H时,螺旋不可旋得太紧,以免接触压力过大引起透镜弹性形变,甚至损坏透镜。
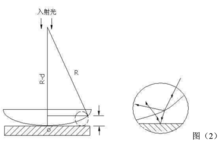 当一曲率半径很大的平凸透镜的凸面与一磨光平玻璃板相接触时,在透镜的凸面与平玻璃板之间将形成一空气薄膜,离接触点等距离的地方,厚度相同。如图2所示。若以波长为λ的单色平行光投射到这种装置上,则由空气膜上下表面反射的光波将互相干涉,形成的干涉条纹为膜的等厚各点的轨迹,这种干涉是一种等厚干涉。
当一曲率半径很大的平凸透镜的凸面与一磨光平玻璃板相接触时,在透镜的凸面与平玻璃板之间将形成一空气薄膜,离接触点等距离的地方,厚度相同。如图2所示。若以波长为λ的单色平行光投射到这种装置上,则由空气膜上下表面反射的光波将互相干涉,形成的干涉条纹为膜的等厚各点的轨迹,这种干涉是一种等厚干涉。
在反射方向观察时,将看到一组以接触点为中心的亮暗相间的圆环形干涉条纹,而且中心是一暗斑(图3(a))如果在透镜方向观察,则看到的干涉环纹与反射光的干涉环纹的光强分布恰成互补,中心是亮斑,原来的亮环处变为暗环,暗环处变为亮环(图3(b))这种干涉现象最早为牛顿所发现,故称牛顿环。
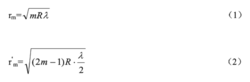 设透镜L的曲率半径为R,形成的m级干涉暗条纹的半径为
设透镜L的曲率半径为R,形成的m级干涉暗条纹的半径为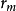 ,形成的m级干涉亮条纹的半径为
,形成的m级干涉亮条纹的半径为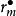 ,不难证明图一。
,不难证明图一。
以上两式表明,当λ已知时,只要测出第m级暗环(或亮环)的半径即可算出透镜的曲率半径R,相反,当R已知时,即可算出λ。但由于两接触镜面之间难免附着尘埃,并且在接触时难免发生弹性形变,因而接触处不可能是一个几何点,而是一个圆斑,所以近圆心处环纹比较模糊和粗阔,以致难以确切判定环纹的干涉级数m,即干涉环纹的级数和序数不一定一致。这样如果只测量一个环纹的半径,计算结果可能有较大的误差。为了减少误差,提高测量精度,必须测量距中心较远的、比较清晰的两个环纹的半径,例如测量出第m1个和第m2个暗环(或亮环)的半径(这里m1、 m2均为环序数,不一定是干涉级数),因而图一(1)式应修正为
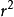 =(m+j)Rλ——————(3)
=(m+j)Rλ——————(3)
式中m为环序数,(m+j)为干涉级数(j为干涉修正值),于是如图3的(4)所示。
上式表面,任意两环的半径平方差和干涉级以及环序数无关,而只与两个环的序数之差(m2-m1)有关。因此,只要精确测定两个环的半径,由两个环的半径的平方差值就可准确地算出透镜的曲率半径R,即图3的(5)和(6).
补充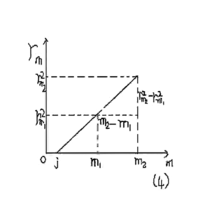
由(3)式可以知道,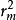 与m直线关系,如图4,其斜率为Rλ,因此,也可以测出一组暗环(或亮环)半径
与m直线关系,如图4,其斜率为Rλ,因此,也可以测出一组暗环(或亮环)半径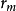 和它们相应的环序数m,作
和它们相应的环序数m,作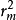 -----m的关系曲线,然后从直线的斜率算出R。2
-----m的关系曲线,然后从直线的斜率算出R。2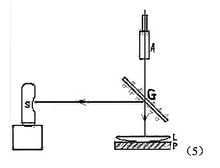




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国