概念
重整化群是一个在不同长度标度下考察物理系统变化的数学工具。标度上的变化称为“标度变换”。重整化群与“标度不变性”和“共形不变性”的关系较为紧密。共形不变性包含了标度变换,它们都与自相似有关。在重整化理论中,系统在某一个标度上自相似于一个更小的标度,但描述它们组成的参量值不相同。系统的组成可以是原子,基本粒子,自旋等。系统的变量是以系统组成之间的相互作用来描述。
基本原理以量子电动力学为例。利用Feynman展开的微扰论方法,我们计算一个物理量,比如电子之间的散射率,会得到一个按照耦合常数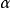 展开的级数,每一项的系数是粒子动量
展开的级数,每一项的系数是粒子动量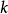 的积分式。这样的积分式会出现紫外发散,即
的积分式。这样的积分式会出现紫外发散,即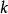 允许的取值可以到无穷大时,系数趋向于正或负无穷,这使得整个理论失去意义。
允许的取值可以到无穷大时,系数趋向于正或负无穷,这使得整个理论失去意义。
为了克服这一困难,人们引入了重整化方法。用这个方法,我们首先对所有的积分作紫外截断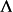 ,从而得到有限结果。显然,这样得到的展开系数将与截断
,从而得到有限结果。显然,这样得到的展开系数将与截断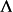 有关。但是,在连续场论中这个截断是人为引入的,物理上并不存在。为了解决这个问题,对于任意
有关。但是,在连续场论中这个截断是人为引入的,物理上并不存在。为了解决这个问题,对于任意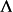 ,我们要求可以重新定义一个相应的耦合常数
,我们要求可以重新定义一个相应的耦合常数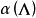 ,使得计算最后给出的物理量与
,使得计算最后给出的物理量与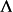 无关。在量子电动力学和其他可重整的理论中,这是可以做到的。换句话说,对于微扰展开的任意级次,可以定义该系统的一系列和截断
无关。在量子电动力学和其他可重整的理论中,这是可以做到的。换句话说,对于微扰展开的任意级次,可以定义该系统的一系列和截断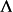 相关的参数,使得系统在动量远小于
相关的参数,使得系统在动量远小于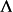 时的物理性质和
时的物理性质和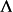 无关。由于实际的
无关。由于实际的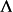 最后要取为无穷大,也就是说,系统在任意有限动量上的物理性质和
最后要取为无穷大,也就是说,系统在任意有限动量上的物理性质和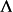 无关,于是,我们要求理论具有这样的不变性:当
无关,于是,我们要求理论具有这样的不变性:当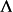 改变一个比例
改变一个比例 时,耦合常数将作相应的变化,而最后给出的结果将是与
时,耦合常数将作相应的变化,而最后给出的结果将是与 无关的。这也就导致了重整化群的想法。也就是说,对于
无关的。这也就导致了重整化群的想法。也就是说,对于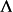 改变一个比例
改变一个比例 这种变换的全体有一个类似群的结构,即满足组合律;先改变
这种变换的全体有一个类似群的结构,即满足组合律;先改变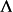 比例为
比例为 ,再接着改变
,再接着改变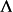 比例为
比例为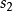 得到的耦合常数等于作一次改变
得到的耦合常数等于作一次改变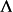 比例为
比例为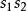 得到的耦合常数。但严格说起来,这并不是一个群,而是一个所谓的半群。原因是在上述定义下,我们无法定义逆变换。
得到的耦合常数。但严格说起来,这并不是一个群,而是一个所谓的半群。原因是在上述定义下,我们无法定义逆变换。
现在,我们把 写成
写成
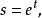 并令
并令
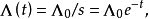 其中
其中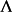 是一个固定的数。如上所述,为使得最后结果有物理意义,我们要让耦合常数
是一个固定的数。如上所述,为使得最后结果有物理意义,我们要让耦合常数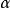 也作相应的改变,即
也作相应的改变,即 也随参量
也随参量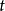 改变。并令
改变。并令
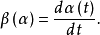 由此,我们可以定义所谓
由此,我们可以定义所谓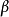 函数。它是重整化群理论中最重要的一个物理量,决定了相应的相互作用在整个理论框架下所起的作用。1
函数。它是重整化群理论中最重要的一个物理量,决定了相应的相互作用在整个理论框架下所起的作用。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国