[科普中国]-传播子

概念

图中的虚光子对应传播子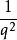 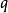， 为虚光子的4-动量。例如在 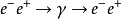湮没过程中，光子传播子的形式为 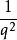，其中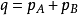 ，由能量-动量守恒给出。

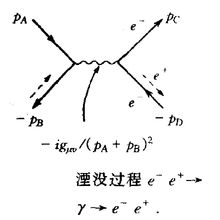
不考虑自旋，质量为 的粒子的传播子为 。例如，在图1中有两个顶点，结果可写为微扰展开中的二阶项

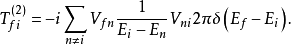
这里不讨论具体的细节，只简单地看一下如何实现传播子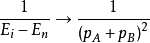。1

基本原理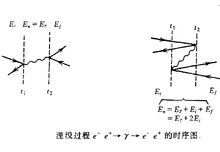

对于图1，有两个可能的时序图，如图2，因而散射有如下形式：

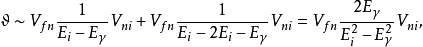式中因子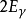与归一化有关。散射幅的这种计算方法是非相对论性的微扰论，顶点的3-动量守恒，但能量不守恒。另外，粒子在质壳上，为了给出传播子，由

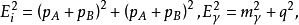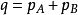因为，有

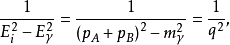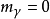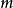其中保持了光子的质量，以便与粒子的传播子作比较。无自旋、质量为的粒子传播子的相对论推广为

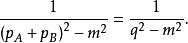
单独看图2中每一个时序图，它不是协变的，但将两图相加，并利用标准的非相对论结果，我们得到了一个Lorentz不变的表达式。

以上的讨论中协变地使用了非相对论微扰论，至关重要的一步是利用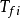的表达式是协变的这一事实。对于无自旋电子的电磁作用，我们明显地导出了它们的形式。与非相对论框架相比较，重要的差别在于能量和3-动量在每一顶点上守恒。这实际上包括了相对论微扰论和Feynman图的讨论。这些部分实质上是技巧性的。电子、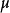子和夸克的自旋为1/2，它们满足Dirac方程而不是Klein-Gordan方程。1