[科普中国]-电荷守恒定律

历史

美国科学家与政治家富兰克林于1747年与朋友通信：

在这里与欧洲，科学家已经发现，并且证实，电火是一种真实的元素或物质种类，不是因摩擦而产生，而是只能从搜集获得。

——本杰明·富兰克林1

学术界归功富兰克林为这定律的创建者。“富兰克林电荷守恒定律”表明，在任何绝缘系统内，总电荷量不变。2

概念电荷守恒定律是物理学的基本定律之一 。它指出，对于一个孤立系统，不论发生什么变化 ，其中所有电荷的代数和永远保持不变。电荷守恒定律表明，如果某一区域中的电荷增加或减少了，那么必定有等量的电荷进入或离开该区域；如果在一个物理过程中产生或消失了某种电荷，那么必定有等量的异号电荷同时产生或消失。

电荷的多少称为电荷量，常简称为电量，故电荷守恒定律又称电量守恒定律。在国际单位制中，电荷量的单位是库仑，用字母Q表示，单位为C。通常正电荷的电荷量用正数表示，负电荷的电荷量用负数表示。

原则守恒定律建立于一个基础原则，即电荷不能独自生成与湮灭。假设带正电粒子接触到带负电粒子，两个粒子带有电量相同，则因为这接触动作，两个粒子会变为中性，这物理行为是合理与被允许的。一个中子，也可以因贝塔衰变，生成带正电的质子、带负电的电子与中性的反中微子。但是，任何粒子，不可能独自地改变电荷量。物理学明确地禁止这种物理行为。更仔细地说，像电子、质子一类的亚原子粒子会带有电荷，而这些亚原子粒子可以被生成或湮灭。在粒子物理学里，电荷守恒意味着，在那些生成带电粒子的基本粒子反应里，虽然会有带正电粒子或带负电粒子生成，在反应前与反应后，总电荷量不会改变；同样地，在那些湮灭带电粒子的基本粒子反应里，虽然会有带正电粒子或带负电粒子湮灭，在反应前与反应后，总电荷量绝不会改变。

电磁学表述流入某体积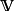的净电流为

；

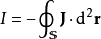其中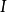，是电流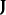，是电流密度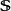，是包围体积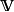的闭曲面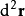，是微小面矢量元素，垂直于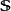从体积内朝外指出。

应用散度定理，将这方程写为

。

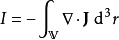总电荷量与体积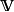内的电荷密度的关系为

。

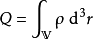电荷守恒要求，流入体积的净电流，等于体积内总电荷量Q的变率：

。

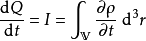所以，。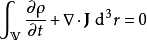

对于任意体积，上述方程都成立。所以，可以将被积式提取出来：

。

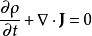电荷守恒方程又称为电荷连续方程。

在十九世纪中期，詹姆斯·麦克斯韦发现安培定律（原本形式）不能满足电荷守恒的要求。于是，他将安培定律的方程加以修正为麦克斯韦-安培方程。由于这动作，麦克斯韦发觉包括这方程在内的麦克斯韦方程组，可以用来描述电磁波的物理行为，并且推导出电磁波以光速传播于自由空间。因此，他正确地断定光波是一种电磁波。更详尽细节，请参阅条目麦克斯韦方程组。

确实无误，麦克斯韦方程组已概括了电荷守恒方程。思考麦克斯韦-安培方程，

；

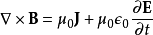其中，B是磁场，是磁常数，是电常数，E是电场。

取这方程的散度，

。

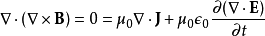应用高斯定律，

。

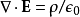所以，电荷守恒成立，

。

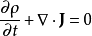属性要使物体带电，可利用摩擦起电、接触起电、静电感应、（感应起电）、光电效应等方法。物体是否带电，通常可用验电器来检验。物体带电实际上是得失电子的结果。这意味着电荷不能离开电子、质子而存在。电荷乃是电子、质子等微观粒子所具有的一种属性。

由摩擦起电和其他起电过程的大量实验事实表明，一切起电过程其实都是使物体上正、负电荷分离或转移的过程中，在这种过程中，电荷既不能消灭，也不能创生，只能使原有的电荷重新分布。由此就可以总结出电荷守恒定律：一个孤立系统的总电荷(即系统中所有正、负电荷之代数和)在任何物理过程中始终保持不变。所谓孤立系统，就是指它与外界没有任何相互作用的系统，是一种理想状态。电荷守恒定律也是自然界中一条基本的守恒定律，在宏观和微观领域中普遍适用。

近代物理实验发现，在一定条件下，带电粒子可以产生和湮没。例如，一个高能光子在一定条件下可以产生一个正电子和一个负电子；一对正、负电子可以同时湮没，转化为光子。不过在这些情况下，带电粒子总是成对产生和湮没，两个粒子带电数量相等但正负相反，而光子又不带电，所以电荷的代数和仍然不变。因此，一个与外界没有电荷交换的系统，电荷的代数和保持不变。它是自然界重要的基本规律之一。

静电学在静电学里，电势乃是相对的，不是绝对的。假设在三维空间的电势为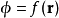，现将电势加上一个常数 c，改为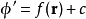，则电场不会改变，这性质称为规范不变性。由于这性质，必需先设定在某参考位置的电势，在其它位置的电势才具有真实物理意义。因此，每一条方程只会涉及到相对电势，不会涉及到绝对电势。

电荷守恒与规范不变性密切相关。这可以用一个思想实验来论述。假设某种过程可以破坏电荷守恒（假若无法永久地破坏，至少可以暂时地破坏）。这过程会在空间里电势为的某位置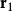生成电荷q，然后将这电荷迁移至在空间里电势为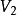的位置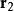，最后将这电荷湮灭。注意到这过程并没有破坏全域电荷守恒定律，只破坏了局域电荷守恒定律。3

现在规定，在任意位置，生成电荷需要输入能量W，湮灭电荷会释出能量W。由于生成电荷或湮灭电荷的位置是任意位置，W不会与相对电势有关。W也不会与绝对电势有关。那么，整个过程会使得系统获得能量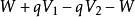。但是，这样做会违反能量守恒。为了遵守能量守恒，必需要求局域电荷守恒。所以，由于规范不变性，电荷守恒定律成立。

实验证据假若电荷不永远守恒，则可能会发生粒子衰变。检验电荷守恒最好的实验方法就是寻找这些粒子衰变。至今为止，物理学者尚未能找到任何这类衰变。例如，对于电子衰变为中微子与光子的反应，物理学者试着侦测这反应产生的高能光子：4

|| ||

但是，有理论提出，即使电荷不永远守恒，这种生成高能光子的衰变反应也永远不会发生。当然，也有实验试着侦测不产生高能光子的衰变，或者一些比较不寻常的电荷破坏过程，例如，电子可能会自发变成正电子、电子移入其它维度。最优良的实验值限为

|| ||