[科普中国]-电场能量密度

理想平行班电容器内的静电能及能量密度

一平行板电容器的两极间距d比极板面的线度小很多时，可忽略边缘效应，看成一个无穷大的理想平行板电容器。板间不填充任何介质，加有直流电压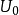 ,则两板间存在均匀电场，电场强度数值为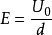

极板上面电荷密度为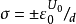 ,极板面积S，电源提供的能量为

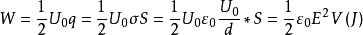
由此可求出电场能量密度为 .

静电学中的能量有些教材讲该结论适合一切电场。平行板电容器的电场只是无数电场中的一个特例, 用该场推导的结论不一定具有普遍性，所以有学者又用其他方法推导公式来验证此结论。下面首先对静电场中的一些能量公式进行分析对比, 指出静电能是电势能、自能或固有能、相互作用能的统称, 静电场的能量就是激发静电场的带电体系总的静电能。

电势能、相互作用能静电场是保守力场或势场, 检验电荷q0在静电场中某点p 的电势能可表示为1

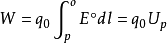
式中Up 是静电场中p 点的势能。q0 的电势能实际上是检验电荷和静电场(或产生静电场的场源电荷)构成的带电体系所共有的,所以电势能也称带电体系的相互作用能, 又称带电体系的静电能, 属于该带电体系总静电能的一部分.

自能一个孤立的带电体其静电能称为自能或固有能。用做功的方法来定义,设物体带电量为Q 时, 其电势为U , 则带电体整个荷电过程中, 外界反抗电场力所做的功转化为该带电体的静电自能W , 写成

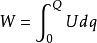
同相互作用能比较可知, 带电体的自能本质上是带电体上各部分电荷之间的相互作用能。1

电荷连续分布的带电体系的静电能这种体系可以是一个带电体或若干个带电体, 各带电体的自能再加上它们之间的相互作用能便是整个带电体系的总静电能。设带电体的体积为V , 电荷分布的体密度为ρ(x , y , z), 其总静电能为:

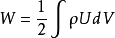
积分遍及带电体全部体积V 。U 为被积带电体体积元所在处的电势, 此电势是所有其它带电体及被积带电体积元电荷共同产生的。

静电场能量密度的两种推导方法用电力线管推导电场能量及其能量密度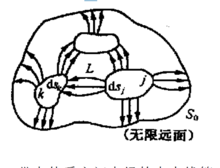：从带电体系的总静电能出发, 导出带电体系的静电场能量, 进而得到静电场的能量密度。设有m 个电荷连续分布的带电体构成带电体系。导体1 的电荷为Q1 , 导体2 的电荷为Q2 ...导体m 的电荷为Qm。设想电场空间的电力线由无限多电力线管构成, 每一个电力线管在导体表面上的面积为ds , 如下图 所示。

对于任意考察的电力线管L , E·ds 为一定值, 等于通过电力线管截面的电通量。其中E 是电力线管中各点的电场强度, ds 为场强E 所在点的电力线管的截面积, ds 指向电力线方向。对于连接导体j 和导体k 的任意电力线管L , dsj 沿电力线方向, dsk 与电力线方向相反, 如右图所示。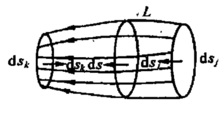

以上讨论的是真空中的静电场, 对于线形电介质中的静电场, 可以考虑电位移线管,对于任一考察的电位移线管,都可以得到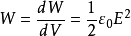

详细推导过程请查看文献‘用电力线管推导电场能量及电场能量密度’。2

运用元电容概念分析在任意自由空间中的静电场可用电通量管来描述电场的结构，每个电通量管内电通量线的根数是固定的，整个空间是由无穷个小点通量馆组成的。如图所示。可假想每个电通量管是无数个理想平行板电容器即元电容串联的集合。由于空间不存在自由电荷，可假设通量管中元电容极板的每个平板在它两个面上有相等而符号相反的电荷，因而在电通量管中不存在净电荷。

对每个元电容不许考虑边缘效应，因为每个局部元电容中的场被周围元电容中的场加以保护。这样任意一个自由空间是由无数个元电容组构成的一个电容结构，而每个元电容都相当于一个无限大平行板电容器。所以用理想平行板电容器的均匀场研究空间电场能量分布具有普遍意义。