[科普中国]-第二类永动机

第二类永动机研究的历史

历史上首个成型的第二类永动机装置是1881年美国人约翰·嘎姆吉为美国海军设计的零发动机，这一装置利用海水的热量将液氨汽化，推动机械运转。但是这一装置无法持续运转，因为汽化后的液氨在没有低温热源存在的条件下无法重新液化，因而不能完成循环。

1820年代法国工程师卡诺设计了一种工作于两个热源之间的理想热机——卡诺热机，卡诺热机从理论上证明了热机的工作效率与两个热源的温差相关。德国人克劳修斯和英国人开尔文在研究了卡诺循环和热力学第一定律后，提出了热力学第二定律。这一定律指出：不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响。热力学第二定律的提出宣判了第二类永动机的死刑，而这一定律的表述方式之一就是：第二类永动机不可能实现。1

对第二类永动机的一般认识许多“发明者”喜欢选择性地利用一些效应，同时选择性地忽略另一些效应，从而在理论上虚构出一些“理论上成立”的永动机模型。这些模型只在“理论上”成立，而在现实中不成立，因为在现实中，被“发明者”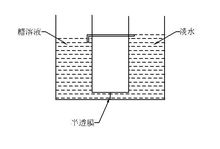忽略的另一些效应会抵消他们选择的效应产生的不平衡，从而使模型无法运转。例如，右边是一个利用反渗透与扩散原理的第二类永动机方案。

“发明者”认为在同等深度下糖溶液的压强必定大于淡水的压强，而反渗透要求的条件是：压力差>渗透压。根据渗透压公式：π=cRT，可知，渗透压只与浓度和温度有关，与深度无关。所以随着方案深度的上升，糖水与淡水的压力差也在上升，而渗透压不变。一个是持续增加，另一个是不变，所以最终会在某一个深度下，压力差会大于渗透压，就能反渗透。糖水中的水就能反渗透到淡水那边，从而提升淡水的水位，从而得到重力势能。但是反渗透下，糖水会持续的变成上淡下浓（由于糖的分子被半透膜挡下来），所以为了让方案持续运动，需要借助扩散现象。扩散现象是只需要温度大于绝对零度，并且出现压力差、温度差、浓度差，随意出现一个时就会发生。

反渗透让糖水浓度变化，而扩散现象恢复变化。

“发明者”在理论上推导过程中，选择了“糖水密度比水大，压强随水深增大比纯水压强随深度增大快”这一效应。然而，他们却忽略了另一效应，即玻尔兹曼分布。对趋向均匀扩散的粒子受到保守力场作用时，一方面扩散现场使粒子趋向于在空间中均匀分布，另一方面保守力场的作用使粒子趋向于向势能低的区域聚集，最后两方面综合作用结果，就是粒子呈玻尔兹曼分布，粒子扩散至充满空间，但是势能低的区域粒子密度大，势能高的区域密度小。例如，气体在地球引力作用下，就不是均匀分布，而是高空中空气比较稀薄，低空中空气比较稠密（虽然在高度差别不大的情况下，分子密度变化很小）。同样的道理，糖分子在糖水中的分布，在分子扩散和重力综合作用下，最后呈现上稀下浓的玻尔兹曼分布。那么根据渗透压π=cRT，当深度较大时，糖水浓度c也增大，所以糖水底部的渗透压比顶部渗透压高。这渗透压增大的部分，恰好抵消前述“发明者”选择的“压强差随深度增大”的效应。最终该模型不能运转。所以“发明者”只能在理论上论证该模型是成立的第二类永动机，但实际上做不出来。因为不管他忽略还是不忽略，承认还是不承认，玻尔兹曼分布都在现实中存在，从而导致他的模型无法运转。

除此之外，还有很多依靠选择性地利用一些效应而忽略另一些效应的“理论上”成立的第二类永动机模型。最著名的就是“费曼棘轮”。“发明者”选择性地认为棘轮会布朗运动，而同时选择性地忽略棘爪也会有布朗运动，从而在理论上论证模型可行，但现实中是做不出来的，因为不管他忽略或不忽略，承认还是不承认，棘爪都会有布朗运动。1

近几年对第二类永动机的研究1、第二类永动机研究的群体与第一类永动机的研究群体不同，第二类永动机的研究者大多受到高等教育，甚至是专业的科研工作者。例如上海交大的副教授傅信镛，中科院生物物理所的徐业林，涟水县教育局的朱顶余、何沛平，山东枣庄的中学物理教师’贾传瑞，业余研究者席加站、崔立等都受过高等教育。

2、第二类永动机不是科研的禁区热力学第二定律作为一条经验定律从来没有经过严格的理论证明，没有寻找到热功逆转的方式，是否就是永远找不到？谁能下这个断言？即使下了这个断言又是可靠的吗？很明显不能，因为从逻辑上说不过去。因此我们不能把第二类永动机当做科学研究的禁区。寻找第二类永动机即使失败了，也从各个方面加深了人类对热力学的认识，也不是无用功。

3、最新的研究成果由热力学第二定律的建立是对微观粒子的运动从有序到无序的方向性推断确立的。因此研究者也是从微观粒子运动的方向性入手进行研究的。

1、傅信镛的磁电偏转电池。在真空中有两个电极，很明显由于电子运动的无序性，某些能量高的电子能够从电极上跑出来，在电极上加磁场，那么由于磁场的偏转作用可以使一个电极带正电，一个电极带负电。傅信镛的研究曾获得钱学森的支持。

2、徐业林的无偏二极管。

攻读现代物理学出身的徐业林研究员，在经历数十年的科学探索中，制成的“无偏二极管”是一种非常巧妙的微电子器件。它将两块金属片，一块为很平的铬层，另一块为有着很多小坑的铬层，中间夹着半导体的硅层。它是利用环境温度，将半导体中导电电子无序的热运动，转化成有序的电流。无偏二极管与负载电阻构成一个回路，回路中有一开关，平时总是断开的，即与环境温度是相通的、相等的。如果将它关闭，无偏二极管的温度即行下降。可见，无偏二极管是通过环境温度对二极管本身温度下降的补偿，利用巧妙的微电子结构而不断运作的。

3、贾传瑞的单一热源热电池。

金属板单一热源热电池。

在同一温度下，不同金属的脱出功不同，这样相对放置的两块金属板，达到发射和吸收电子的平衡时一块金属板带正电，一块金属板带负电。

实验见《发明与创新》杂志2005年第5期《非温差电现象的实验探讨》一文。

半导体单一热源热电池

利用半导体结电场的不对称性，可以制成比金属板效率高的半导体热电池。贾传瑞的单一热源热电池已申请专利。由于传统认识的影响，虽然给出了数学推导， 但仍然未获授权。

4、热力学第二定律在引力场中不成立获得确定性证明

热会自发的从高温物体传给低温物体，而不是相反也就是说热具有自发拉匀的趋势。在引力场中是否也一定成立呢？最新研究发现在引力场中空气的温度会自发的存在一定的温度梯度。并且贾传瑞，何沛平、朱顶余，席加站分别用不同的方式进行了数学证明。毫无疑问只要在引力场中空气存在温度梯度是自发过程，那么热力学第二定律在引力场中就不成立。因为我们可以把大气温差用温差电池发电。大气和温差电池就组成了永动机系统。

具体数学分析见《发明与创新》杂志2005年第六期《对热力学第二定律的再思考》一文。

5、确定成立的析盐永动机

上面一个利用反渗透与扩散原理的第二类永动机方案，被持有传统观点的人士否定了。毫无疑问提出利用反渗透与扩散原理的第二类永动机方案的人没有想到重力场对糖水浓度会有影响。但否定的人并没有说明影响到底有多大，通过数字说明影响到足以使反渗透不可发生。其实我们可以简化思维：同等高度的的糖水和纯水在糖水达到扩散平衡时存不存在某一深度恰好压强差大于渗透压的情形。如存在，则半透膜两侧的反渗透一旦发生则永不停止。如不存在，则“同等高度的的糖水和纯水在糖水达到扩散平衡时，任意深度两侧压强差小于渗透压”成为定理。

其实这里有一个更容易理解的析盐永动机。我们知道食盐的密度大于水的密度，食盐放入水中会下沉，重力会对外做功，食盐在海底溶解，然后扩散上升，在海平面我们把食盐和水分离，然后再把食盐放入海底·······这样我们会得到净功吗？为简化计算，我们假设海水是饱和食盐水。一吨水可溶解360千克食盐，如果以最节能的方式把食盐和水分离需1.498X10000000焦耳的能量（低压蒸馏水汽化的能量由水蒸气冷凝放热补充，外界所做的功是用于补充食盐水和纯水的饱和蒸气压之差所做的功），360千克食盐沉入10000米的海底可做功1.36X10000000焦的功。沉入20000米海底可做功2.72X10000000焦耳。因此如果海水足够深是可以实现热功逆转的。但由于地球上最深的马里亚纳海沟只有11000米，因此析盐永动机也只是理论上的第二类永动机。

6、渗透式永动机如右图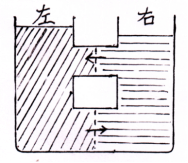右图左侧为密度大于水的溶液，而右侧为水。上、下两个连通分别装有半透膜。假设其中一个半透膜两侧存在渗透平衡，则另一个半透膜两侧必不平衡。

假如：设上面半透膜两侧存在平衡P左=P渗+P右，则下面的半透膜两侧必不平衡：

P左+ρ溶液g△h>P渗+P右+ρ水g△h。因此这个装置为永不平衡的结构。图中箭头为水分子的运动方向。

7、蒸发式永动机

右图一个回型容器里有个微孔筛，左侧为水，而两微孔筛之间为空气。则下面筛孔的向上凸起的液面的内压强大于外压而易于蒸发，而上面的筛孔液面向内凹，内压强小于外压强而利于水蒸气液化，这样就造成了水分子的单向运动。

8、凸透镜永动机

在一个恒温的正方形黑盒子里放一个凸透镜，在放大镜的焦点位置附近放一个黑体，由于凸透镜对红外线的聚光作用，黑体的温度会比环境温度要高，造成盒子内的空气永不停息的对流运动。此时凸透镜自动的形成了逆熵。2

相关资料1、热传导的方向性

热传导的过程是有方向性的，这个过程可以向一个方向自发地进行，但是向相反的方向却不能自发地进行。

**2、**热力学第二定律

热力学第二定律有多种表述，下面给出常见的两种。

一种表述是：不可能使热量由低温物体传递到高温物体，而不引起其他变化。这是按照热传导的方向性来表述的。

另一种表述是：不可能从单一热源吸收热量并把它全部用来做功，而不引起其他变化．这是按照机械能与内能转化过程的方向性来表述的，它也可以表述为：第二类永动机是不可能制成的。

3、能量耗散

能量耗散是从能量转化的角度反映出自然界中的宏观过程具有的方向性。2