[科普中国]-弧度制

发展历程

在研究弧度制发展时，我们必须谈到三角学和角，因为弧度制是依托它们二者存在的。依据三角学在数学研究中的地位，笔者认为三角学的发展可以分为萌芽阶段、传播阶段和确立阶段三个阶段。萌芽阶段从公元前约300年古巴比伦时期开始到公元640年希腊古代数学落幕为止，这段时期由于天文学的需要，三角学受到学者们的重视，它是天文学的一部分；传播阶段从公元640年希腊古代数学落幕后到15世纪文艺复兴开始前为止，这段时期三角学在不同地区传播，虽然其研究内容本质与萌芽阶段时相比没有区别，但它逐渐脱离天文学，成为了数学的一个分支；确立阶段是从文艺复兴开始至今，在微积分等新兴数学力量的崛起下，三角学逐渐成为了其他数学分支中的一部分，而在此期间，弧度制成为了度量角的主要单位。

18世纪以前，人们一直是用线段的长来定义三角函数的。弧度定义的提出，是数学家Roger Cotes在1714年提出的，作为一种对角度的描述，使得对三角函数的研究大为简化。中学数学教科书中都把radian译作“弧度”。 1881年，学者哈尔斯特(G．B．Halsted)等用希腊字母ρ表示弧度的单位．1907年，学者包尔（G．N．Bauer)用r表示；1909年，学者霍尔(A．G．Hall)等又用R来表示，例如将单位弧度（角度制1°）写成（π/180）rad，人们习惯把弧度的单位省略。1

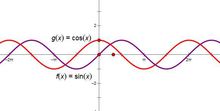
基本思想弧度制的基本思想是使圆半径与圆周长有同一度量单位，然后用对应的弧长与圆半径之比来度量角度，这一思想的雏型起源于印度。那么半圆的弧长为π，此时的正弦值为0，就记为sinπ= 0，同理，1/4圆周的弧长为π/2，此时的正弦为1，记为sin(π/2)=1。从而确立了用π、π/2分别表示半圆及1/4圆弧所对的中心角。其它的角也可依此类推。1

角度与弧度角度分：在任意一个角一边所对应的射线情况下，逆时针旋转所形成的角称为正角；顺时针转动所形成的角称为负角；射线未作任何旋转，仍留在原来位置，那么我们也把它看成一个角，叫做零角。1

弧度分：正角的弧度值是一个正量（正实数），负角的弧度值是一个负量（负实数），零角的弧度值是零。1弧度制能使角的集合与实数集合R存在一一对应关系：每一个角都对应唯一的一个实数。

角度制，就是用角的大小来度量角的大小的方法。在角度制中，我们把周角的1/360看作1度，那么，半周就是180度，一周就是360度。由于1度的大小不因为圆的大小而改变，所以角度大小是一个与圆的半径无关的量。

弧度制，顾名思义，就是用弧的长度来度量角的大小的方法。单位弧度定义为圆周上长度等于半径的圆弧与圆心构成的角。由于圆弧长短与圆半径之比，不因为圆的大小而改变，所以弧度数也是一个与圆的半径无关的量。角度以弧度给出时，通常不写弧度单位，有时记为rad或R。

换算

一个完整的圆的弧度是2π，所以：

2π rad = 360°，1 π rad = 180°，1°=π/180° rad ，1 rad = (180/π)°≈57.30°=57°18ˊ1

有关公式弧长公式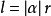

上式中，l为弧长，α为角度（弧度制），r为半径。

推导：由弧度定义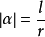得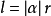

面积公式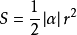

上式中，S为面积，α为角度（弧度制），r为半径。

推导：（角度制角度为n°）由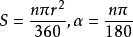，将α代入，得到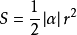

相关物理量角速度做圆周运动的物体在单位时间内所走的弧度即为角速度。符号：ω，单位：弧度每秒（rad/s）。定义公式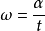：(α为所走过弧度，t为时间）。

由角速度、线速度（速率）的定义公式及弧长公式可以推出角速度与线速度的关系式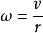：（r为半径）2

周期做周期运动的物体完成一次周而复始的运动所需的时间即为周期。符号：T，单位：秒（s）。

在匀速圆周运动中，周期T与角速度ω有关，关系式为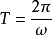。2

意义弧度制之所以能成为当今数学主要的角的单位制度，主要原因有二：

(一)使进位制统一。在古巴比伦以及古希腊时期，数学家在研究天文学问题时，普遍习惯使用60进制对角进行度量，为了进位制的统一，也用60进制度量弦长和弧长。此时，角度制满足了这种需求。而随着历史的发展，10进制取代了60进制成为了度量长度的主要进位制。为了保持进位制的统一，自然地也将角的进位制换成10进制。弧度制满足了这一需求，而且可以与角度制进行一一对应的换算，与原有数学系统相容．这样，在查阅三角函数表时就可以看到用统一进位制表示的数，便于数与数之间的对比，提高解决问题的效率。

(二)简化微积分创立后公式的计算．弧度制大约直到18世纪才被提出来，它的提出是受到微积分等近代数学发展的推动的。在弧度制下，与三角函数有关的一些公式在形式上均比角度制下有很大的简化。正是因为这样的优越性，弧度制才逐渐被数学界普遍接受和广泛使用3。