[科普中国]-三角形数

定义

它有一定的规律性，排列如下(构成图)，像上面的1、3、6、10、15等等这些能够表示成三角形的形状的总数量的数，叫做三角形数。

一定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为三角形数。比如10个点可以组成一个等边三角形，因此10是一个三角形数：

x

x x

x x x

x x x x

x x x x x

开始个18个三角形数是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153、171……（OEIS中的数列A000217）

第n个三角形数的公式是 或者 。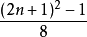

第n个三角形数是开始的n个自然数的和。

所有大于3的三角形数都不是质数。

开始的n个立方数的和是第n个三角形数的平方（举例：1 + 8 + 27 + 64 = 100 =102）

所有三角形数的倒数之和是2。

任何三角形数乘以8再加1是一个平方数。

一部分三角形数（3、10、21、36、55、78……）可以用以下这个公式来表示：n × (2n + 1)；而剩下的另一部分（1、6、15、28、45、66……）则可以用n × (2n - 1)来表示。

一种检验正整数x是否三角形数的方法，是计算：。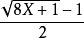

如果n是整数，那么x就是第n个三角形数。如果n不是整数，那么x不是三角形数。这个检验法是基于恒等式8Tn + 1 = S2n + 1.

特殊的三角形数

55、5,050、500,500、50,005,000……都是三角形数。

第11个三角形数（66）、第1111个三角形数（617,716）、第111,111个三角形数（6,172,882,716）、第11,111,111个三角形数（61,728,399,382,716）都是回文式的三角形数，但第111个、第11,111个和第1,111,111个三角形数不是。

和其他数的关系

四面体数是三角形数在立体的推广。

两个相继的三角形数之和是平方数。

三角平方数是同时为三角形数和平方数的数。

三角形数属於一种多边形数。

所有偶完美数都是三角形数。

任何自然数是最多三个三角形数的和。高斯发现了这个规律。他在1796年7月10日在日记中写道：EYPHKA! num = Δ + Δ + Δ

构成图o n=1 s=1

o o n=2 s=3

o o o n=3 s=6

o o o o n=4 s=10

o o o o o n=5 s=15

……

根据自然数列的求和公式，对于第n项的三角形数，可以得到其计算公式为：。

应用1)前n个三角形数的和:T(n)=s(1)+s(2)+…+s(n)

由，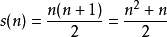

得到:.。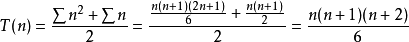

2)判断一个数是否为三角形数:对任给一个正整数K，则若为三角形数,有: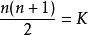得:n*(n+1)=2K。

从而:[即2K开根号]