在统计学,统计决策理论和经济学中,损失函数是指一种将一个事件(在一个样本空间中的一个元素)映射到一个表达与其事件相关的经济成本或机会成本的实数上的一种函数。更通俗地说,在统计学中损失函数是一种衡量损失和错误(这种损失与“错误地”估计有关,如费用或者设备的损失)程度的函数。
简介定义在乘积空间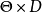 上的函数
上的函数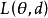 称为损失函数,如果它满足如下两个条件:
称为损失函数,如果它满足如下两个条件:
(1)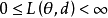 对任意的
对任意的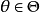 和
和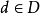 成立;
成立;
(2)对任意固定的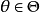 ,
,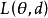 作为 d 的函数是
作为 d 的函数是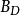 可测的。
可测的。
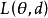 表示当自然解处于状态
表示当自然解处于状态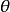 时(参数的真实值为
时(参数的真实值为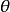 ),人们采取决策(行动)d 所造成的损失。
),人们采取决策(行动)d 所造成的损失。
若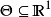 即
即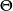 是一堆实数空间上的子集,则称形如
是一堆实数空间上的子集,则称形如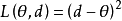 的损失函数为平方损失函数,称形如
的损失函数为平方损失函数,称形如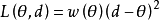 的损失函数为加权平方损失函数,其中
的损失函数为加权平方损失函数,其中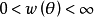 。若
。若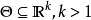 ,即
,即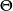 是 k 维实数空间上的子集。设 Q 为
是 k 维实数空间上的子集。设 Q 为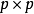 的正定矩阵。则称形如
的正定矩阵。则称形如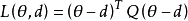 的损失函数为二次损失函数,其中 “T” 表示矩阵转置。二次损失函数关于偏差
的损失函数为二次损失函数,其中 “T” 表示矩阵转置。二次损失函数关于偏差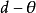 是非对称的损失函数
是非对称的损失函数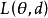 称为非对称的损失函数。1
称为非对称的损失函数。1
应用损失函数是描述系统在不同参数(parameter)值之下的损失。要应用损失的函数,其损失必须是通过某种媒介可以衡量的。损失函数在实践中最重要的运用,在于协助我们通过过程的改善而持续减少目标值的变异,并非仅仅追求符合逻辑。
损失函数并非一定是对称的。有时候其中一边很陡峭,有时候则两边都很陡峭。举例而言,为了使钢片较容易焊接,需要加入钶。但钶的加入量如果低于必须量,纯粹是浪费,对焊接一点益处都没有。然而钶用量如高于十万分之一,也是一种浪费,所增加的利益相当有限。戴明博士曾在《企业研究的样本设计》(Sample Design in Business Research)一书内,列示了一个实际的损失函数。它显示我们只需要尽量靠近样本的最优组合就行了,只要非常接近就可以了。
实际应用案例一某个工厂人员的产出,以每小时多少元来计算,而损失函数所显示的,是产出以室内通风条件而改变的情形。厂内工作的每个人,都有自己的损失函数。为了简化说明,假设每个人的损失函数均为一条抛物线,其底部一点代表产出值最大时的通风条件,把所有人员的损失函数进行叠加,公司整体的损失函数也必然是一条抛物线。如果通风条件偏离这个最佳水准,就会有额外损失发生。该抛物线与横轴相切时,切点的左右各有一小段与横轴几近重合。也就是说,有最适点偏离一小短距离,损失小到可以忽略不计。因此,当室内通风条件稍稍偏离均衡点,发生的损失可以忽略不计。但是远离均衡点时,总是有人必须支付这损失。如果我们能够导出有具体数字的损失函数,我们就可以计算出最优均衡点,在均衡点中最适合的通风条件如何,以及达到要求的费用支出是多少。
案例二以赶火车作为符合规格的例子。假设我们的时间价值为每分钟n元,下图左边的斜线是损失线的斜率;早一分钟到达月台,将让我们损失n元,早两分钟到达损失2n元。另一方面,如果没有赶上火车,我们的损失是M元。迟到半分钟或迟到5分钟损失一样,损失函数直接由零跳到M。
当然问题也可复杂化,例如火车每天离站的时间也有变化,所以也可以画出一个分配图。火车到站时间三个标准差的界限可能是8秒。把问题这样复杂化,对于我们了解和应用损失函数并没有特别大的帮助,因此我们就说到这里。 另一个例子,是参加星期日早上11点15分的礼拜时所碰到的停车问题。教堂的停车场最大负荷是停放50辆车子,但这些车位在10点50分左右仍然客满,因为作完上一场礼拜的车主仍在喝咖啡。等他们一离开,这些空位马上就会被排成长龙等待的车队填满。如果你想占到一个车位,不得不早早去排队。那些晚到的人在这里找不到车位,只能到街上去找,但实际上往往无功而返。所以,上策还是提早一点去等,承受等待的损失而能占到位置。
这项理论也可以应用到任何计划的截止时间上。某人要求必须在截止日期前完成工作,万一未能赶上这个时间,势将使计划延误或出错。为了能准时完成,可以拟定工作内容与步骤的纲要。把个步骤的截止日期 设 定一段期间要比设定为固定的从容,而且有时间作最后的修订,可能把计划做得更好。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国