[科普中国]-偏差

偏差又称为表观误差，是指个别测定值与测定的平均值之差，它可以用来衡量测定结果的精密度高低[1]。在统计学中，偏差可以用于两个不同的概念，即有偏采样与有偏估计。一个有偏采样是对总样本集非平等采样，而一个有偏估计则是指高估或低估要估计的量1。

定义偏差公式：

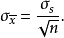
在统计学中常用来判定测量值是否为坏值。精密度是指一样品多次平行测定结果之间的符合程度，用偏差表示。偏差越小，说明测定结果精密度越高。

（测量数据服从正态分布）根据正态分布我们知道，测量值范围在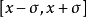 概率为0.6827。在 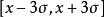的概率是0.997。也就是说，如果测量值的范围不在之上，那么可以判定它是坏值，应当舍去。（x表示测量的平均值，σ表示偏差）

右边公式说明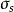： 表示标准误差估算值，也相当于标准误差。

偏差系数

标准差与变量及期望值的大小有关，项目比较时，若某一项目的期望值及标准差均比其他项目大，不能简单地认为标准差大的项目风险就一定大，还应进一步用两者的相对指标进行分析和比较，该相对指标即偏差系数2。

分类所谓“偏差值”，是日本人对于学生智能、学力的一项计算公式值，[(个人成绩－平均 成绩)÷标准差]×10+50=偏差值，也就是自己的分数。偏差分为绝对偏差和相对偏差、标准偏差和相对平均偏差来表示。

1. 绝对偏差：是指某一次测量值与平均值的差异。

2. 相对偏差：是指某一次测量的绝对偏差占平均值的百分比。

3.标准偏差：是指统计结果在某一个时段内误差上下波动的幅度。统计学名词。一种量度数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。

4.平均偏差：是指单项测定值与平均值的偏差（取绝对值）之和，除以测定次数。

5.相对平均偏差：是指平均偏差占平均值的百分率。平均偏差和相对平均偏差都是正值。

偏差与误差误差是测量值与真值之间的差值。用误差衡量测量结果的准确度，用偏差衡量测量结果的精密度；误差是以真实值为标准，偏差是以多次测量结果的平均值为标准。

误差与偏差的含义不同，必须加以区别。但是由于在一般情况下，真实值是不知道的(测量的目的就是为了测得真实值)，因此处理实际问题时常常在尽量减小系统误差的前提下，把多次平行测量值当作真实值，把偏差当作误差。

偏差的实例例：分析铁矿石中铁的质量分数，得到如下数据：37.45，37.20，37.50，37.30，37.25（%），计算测结果的平均值、平均偏差、相对平均偏差、标准偏差。

解：平均值：37.34（%）

各次测量的偏差分别是：0.11,-0.14,0.16,-0.04,-0.09

平均偏差：0.108

相对平均偏差：0.289（%）

标准偏差：0.13（%）

相对标准偏差：RSD=(0.13/37.34)×100%=0.4%

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学