[科普中国]-条件期望

条件期望，又称条件数学期望。为了方便起见，我们讨论两个随机变量X与Y的场合，假定它们具有密度函数f(x,y) ，并以g(y|x) 记已知X=x的条件下Y的条件密度函数，以h(x) 记X的边缘密度函数。定义在X=x的条件下， Y的条件期望定义为：E(Y|X=x)=∫y*g(y|x)dy1。

定义在概率论中，条件期望是一个实数随机变量的相对于一个条件概率分布的期望值。换句话说，这是给定的一个或多个其他变量的值一个变量的期望值。它也被称为条件期望值。

设X和Y是离散随机变量，则X的条件期望在给定事件Y = y条件下是y的在Y的值域的函数

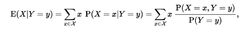
其中，是x处于X的值域。

如果现在X是一个连续随机变量，而在Y仍然是一个离散变量，条件期望是：

其中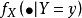， 是在给定Y=y下X的条件概率密度函数。

应用条件数学期望在近代概率论中有着基本重要的作用2，在实际问题中也有很大用处。在两个互有影响的随机变量中，如果已知其中一个随机变量的取值**=y**，要据此去估计或预测另一个随机变量的取值，这样的问题在实际应用中经常会碰到。人们称它为“预测问题”。由上述讨论可知，条件数学期望E( )是在已知(**=**y)发生的条件下，对 的一个颇为“合理”的预测。

一般认为，人的身高和脚印长可当作一个二维正态分布变量来处理。

如果把画在平面的直角坐标系中，它是一条直线，这条直线在一定程度上描写了身高 依赖于 的关系，常常称为是回归直线。在一般情形下，由

E( x，y) 或{x，E( x)}

可以得到平面上的两条曲线，它们称为是回归曲线或简称为回归。

期望的剩余方差还有一点应该指出的是，对于用得最广泛的正态分布来说，可以从例3.27知道，两类回归恰好是一致的。这一事实表明，就正态分布而言，最佳线性估计就是最佳估计。当然，这里“最佳”的意思是指均方差最小

这个均方误差常常称为剩余方差。由上式可知，当 与 间的相关系数| |=1时，剩余方差为零。这时， 可以用方差来准确估计，也就是说 与 之间存在着线性关系。于是我们又一次证明了相关系数是随机变量间线性相依程度的反映。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学