[科普中国]-矛盾方程组

矛盾方程组(contradictory equations)是一种特殊的方程组，在求解范围内无解(解集为空集)的方程组称为这个范围内的矛盾方程组。一个方程组中，若有一个矛盾方程，它必然是矛盾方程组；若方程组中的每个方程都不是矛盾方程，但它们所表达的条件是彼此矛盾的，则它也是矛盾方程组。矛盾方程组是相对的，它与给定的数集有关，若扩大给定的数集，有时可以使一个矛盾方程组转化为有解的非矛盾方程组，即“相容方程组”1。

矛盾方程组及其求解由线性代数理论知，求解线性方程组时，若方程式的个数多于未知数的个数，则方程组往往无解，此类方程组称为矛盾方程组(或超定方程组)。最小二乘法是用来解矛盾方程组的一个常用方法2。

设有矛盾方程组

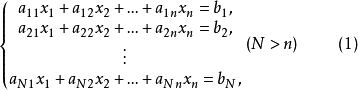或写为

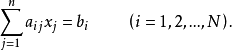
通常找不到能同时满足方程组(1)的解，因此我们转而去寻求在某种意义下的近似解，这种近似解不是指对精确解的近似(因为精确解并不存在)，而是指寻求各未知数的一组值，使方程组(1)中各式能近似相等。这就是用最小二乘法****解矛盾方程组的基本思想。把近似解代入方程组(1)后，只能使各方程式的两端近似相等，不妨记各个方程式两端之差为

并称该差为偏差。按最小二乘原理，采用使偏差的平方和

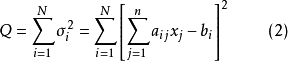达到最小值来作为衡量一个近似解的近似程度的标志2。

相关概念及定理定义1 如果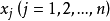 的取值使偏差平方和即式(2)达到最小，则称这组值是矛盾方程组(1)的最优近似解2。

预备知识：

(1)矩阵的秩。设矩阵A有一个n阶子式D，其不等于0，而n+1阶子式皆为0，那么n称为A的秩。

(2)对称矩阵。如果n阶方阵A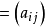 ，满足AT**=A**，即

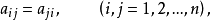则称A为对称矩阵。

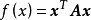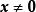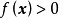(3)正定矩阵。设有实二次型 ，如果对于任何 ，都有 ，则称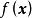 为正定二次型，对称矩阵A是正定的。

如果A为正定矩阵，则A的特征值皆为正的。且A的各阶主子式皆为正。

(4)矩阵的特征值。设A为n阶方阵，如果存在常数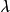及非零的n维列向量X，使AX=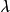X成立，则称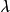是方阵A的特征值。非零向量X称为方阵A的属于特征值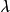的特征向量。

定理1 设n元实函数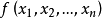 在点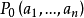 的某个邻域内连续，且有一阶及二阶连续的偏导数，如果

（1）

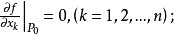
（2）矩阵

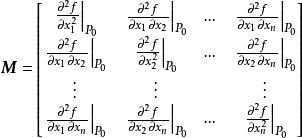是正定矩阵，则 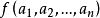是n元实函数 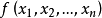的极值。

定理2 设非齐次线性方程组Ax=b的系数矩阵A= ，若rankA=n，则

(1) 矩阵ATA是对称正定矩阵；

(2) n阶线性方程组ATA****x=ATb有唯一的解。

下面我们讨论此二次函数是否存在最小值，若存在，如何求最小值?由高等数学可知，有以下定理。

定理3 设矛盾方程组(1)的系数矩阵A的秩为n，则二次函数

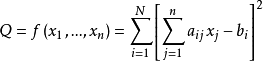一定存在最小值。

通常称线性方程组ATA****x=ATb为正则方程组。只要矛盾方程组(1)的系数矩阵A的秩rankA=n，则由定理3可以得出：

(1)矛盾方程组(1)的最小二乘解存在；

(2)正则方程组ATA****x=ATb有唯一解，此解就是矛盾方程组(1)的最小二乘解。

用最小二乘法求解矛盾方程组Ax=b的步骤归纳如下：

(1)计算ATA和ATb，得正则方程组ATA****x=ATb；

(2)求解正则方程组，得出矛盾方程组的最优近似解2。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学