[科普中国]-代数独立

代数独立是指在抽象代数里，一个域L的子集S若被称做代数独立于一子域K的话，表示S内的元素都不符合系数包含在K内的非平凡多项式。这表示任何以S内元素排成的有限序列α1, ..., αn(没有两个是一样的)和任一系数包含在K的非零多项式P(x1，……，xn)，都会得到 P(α1，……，αn) ≠ 0 的结果。

简介代数独立是指在抽象代数里，一个域L的子集S若被称做代数独立于一子域K的话，表示S内的元素都不符合系数包含在K内的非平凡多项式。这表示任何以S内元素排成的有限序列α1, ..., αn(没有两个是一样的)和任一系数包含在K的非零多项式P(x1，……，xn)，都会得到 P(α1，……，αn) ≠ 0 的结果。特别的是，单元素集合 {α} 若是代数独立于K的话，若且唯若α会是K内的超越数或超越函数。一般而言，和于K代数独立集合的所有元素也必然会是K内的超越数或超越函数，但反之则不必然。

具体内容举例来说，实数R的子集{√π， 2π+1}并不代数独立于有理数Q，当存在一非零多项式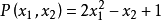 ，当x1代入√π和x2代入2π+1时会变成零。 林德曼-魏尔斯特拉斯定理时常用做证明某些函数会代数独立于有理数。其内容为，当α1，…….，αn为线性独立于有理数的代数数时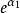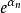， ，……， 便会代数独立于有理数。现在依然没有证明出集合{π, e}是否代数独立于有理数。Nesterenko在1996年证明了{π, eπ, Γ}是代数独立于有理数的。给定一域扩张L/K，我们可以利用佐恩引理来证明总是存在一L的最大代数独立子集于K。甚至，所有个最大代数独立子集都会有相同的基数，称之为此一域扩张的超越次数。1

抽象代数亦称近世代数。研究各种代数系的结构及其性质的分支学科。它是在初等代数基础上经过数系概念的推广，与实施代数运算范围的扩大，从18世纪末萌芽到20世纪30年代，逐步形成现代数学的主要分支之一。

抽象代数是研究以任意对象作为元素的集合，赋予元素间的若干合成法则——即对集合中任意元素a，b有集合中惟一的元素c与之对应——称为运算，并且这些运算满足于特定的一些条件——称为公理。随着集合所赋予的运算及其所满足的公理体系的不同而形成各种不同的代数系，如群、环、域、格、模(包括向量空间)、代数等。

代数系的起源较早，在挪威数学家阿贝尔(Abel，N.H.)证明五次以上方程不能用根式求解的进程中就孕育着群的概念；1830年，年仅19岁的伽罗瓦(Galois，E.)彻底解决了代数方程的根式求解问题，从而引进数域的扩张、置换群、可解群等概念；后来，凯莱(Cayley，A.)在1854年的文章中给出有限抽象群；戴德金(Dedekind，J.W.R.)于1858年在代数数域中又引入有限交换群和有限群；克莱因(Klein，C.F.)于1872年建立了埃尔朗根纲领，这些都是抽象群产生的主要源泉。然而抽象群的公理系统直到1882年凯莱与韦伯(Weber，H.)在Math.Annalen的同一期分别给出有限群的公理定义，1893年韦伯又给出无限抽象群的定义。由于李(Lie，M.S.)对连续群和弗罗贝尼乌斯(Frobenius，F.G.)对群表示的系统研究，对群论发展产生了深刻的影响。同时，李在研究偏微分方程组解的分类时引入李代数的概念，然而，它的发展却是19世纪末和20世纪初，由基灵(Killing，W.K.J.)、外尔(Weyl，(C.H.)H.)和嘉当(Cartan，É.(-J.))等人的卓越工作才建立了系统理论。

域这个名词虽是戴德金较早引入的，但域的公理系统却是迪克森(Dickson，L.E.)与亨廷顿(Huntington，E.V.)于19世纪初才独立给出。而域的系统发展是从1910年，施泰尼茨(Steinitz，E.)的著名论文“域的代数理论”开始的。同期，布尔(Boole，G.)研究人的思维规律，于1854年出版《思维规律的研究》，建立了逻辑代数，即布尔代数。但格论是在1933～1938年，经伯克霍夫(Birkhoff，G.D.)、坎托罗维奇(Канторович.П.В.)、奥尔(Ore，O.)等人的工作才确立了在代数学中的地位。另一方面，1843年，哈密顿(Hamilton，W.R.)引进四元数并奠定了向量代数和向量分析的基础，而四元数系又构成实数域上有限维可除代数。凯莱与西尔维斯特(Sylvester，J.J.)一起建立了代数型的理论，奠定了代数不变量的矩阵理论.。凯莱又是矩阵代数的创始人，他建立了八元数与非结合代数，同时，克利福德(Clifford，W.K.)将八元数(复四元数)及外代数推广到一般克利福德代数，并将其成功地应用于非欧几里得空间中运动的研究。2

域代数学的基本概念之一。即具有两个运算的代数系。设F是至少含两个元的集合，在F中定义了两个二元运算：一个称加法，使F成为加群，它的单位元称为F的零元;一个称乘法，使F的非零元构成一个交换群，加法与乘法满足分配律，此时称F为域。例如，全体有理数、全体实数和全体复数在通常的加法与乘法下都构成域，分别称为有理数域、实数域和复数域。域是许多数学分支研究的基础，尤其对代数、代数数论、代数几何等更为重要。

子域域的特殊子集。若域F的一个子集合为S，对于F的加法与乘法也构成域，则称S为F的子域，而称F为S的扩域。F中至少含一个非零元的子集S是子域的充分必要条件为：对任意a，b∈S恒有a-b和ab-1(b≠0)属于S。例如，有理数域是实数域及复数域的子域，集合：

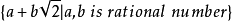是实数域的子域。

超越函数超越函数(Transcendental Functions)，指的是变量之间的关系不能用有限次加、减、乘、除、乘方、开方运算表示的函数。

欧拉把约翰·贝努利给出的函数定义称为解析函数，并进一步把它区分为代数函数（只有自变量间的代数运算）和超越函数（三角函数、对数函数以及变量的无理数幂所表示的函数），还考虑了“随意函数”（表示任意画出曲线的函数）。

如三角函数、对数函数，反三角函数，指数函数，等就属于超越函数。如y=arcsinx，y=cosx，它们属于初等函数中的初等超越函数。

超越函数是指那些不满足任何以多项式作系数的多项式方程的函数。说的更技术一些，单变量函数若为代数独立于其变量的话，即称此函数为超越函数。例如，对数函数和指数函数即为超越函数。 超越函数这个名词通常被拿来描述三角函数，例如正弦、余弦、正割、余割、正切、余切、正矢、半正矢等。

函数的不定积分运算是超越函数的丰富来源，如对数函数便来自代数函数的不定积分。在微分代数里，人们研究不定积分如何产生与某类“标准”函数代数独立的函数，例如将三角函数与多项式的合成取不定积分。

在数学领域中，超越函数与代数函数相反，是指那些不满足任何以多项式作系数的方程的函数，即函数不满足以变量自身的多项式为系数的多项式方程。换句话说，超越函数就是"超出"代数函数范围的函数，也就是说函数不能表示为有限次的加、减、乘、除、乘方和开方的运算。

严格的说，关于变量z的解析函数f(z) 是超越函数，那么该函数是关于变量z是代数独立的。

非超越函数则称为代数函数，代数函数的例子有多项式和平方根函数。

对代数函数进行不定积分运算能够产生超越函数，如对数函数便是在对双曲角围成的面积研究中， 对倒数函数y= k/x不定积分得到的， 以此方式得到的双曲函数sinhx、 coshx、tanhx都是超越函数。

微分代数的某些研究人员研究不定积分如何产生与某类“标准”函数代数独立的函数，例如将三角函数与多项式的合成取不定积分。3

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学