[科普中国]-分离系数法

多项式的分离系数法(method of detached coefficients of polynomials)是多项式四则运算的一种演算形式。对一元多项式进行加、减、乘、除运算时，首先将多项式写成标准形式并按变元降幂或升幂排列，缺项补零占位，然后略去各项的变数字母，分离出各项的系数，仅用系数组成的数列按原运算的意义进行运算，最后将运算所得数列中各数分别配上与之相应项的变数字母的幂作为运算的最后结果，称为多项式的分离系数法。

基本介绍当按竖式计算两个多项式，两个多项式进行加减法运算时，只须对同类项的系数之间进行加减法运算，与变数无关，因此可以把多项式只写出它们的系数进行加减法运算，更为简便，这种方法叫做分离系数法。

举例分析例1计算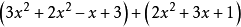 ，可以如下进行：

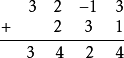结果是 。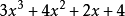

对于乘法或除法也可用分离系数法进行。例如，计算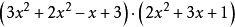

解：

结果是 。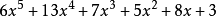

在应用分离系数法进行运算时，注意运算结果的次数，遇有缺项时要空位或补上0，而且两个多项式都要按降幂顺序排列，否则容易出错1。

例2 求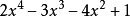 和 的乘积。

**解：**先按 降幂排列，只写出系数，缺项处补充以0，在最后的结果中填入 的适当方幂(从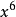 开始，因为积的最高次项的次数是6)。

所以解得 。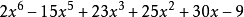

例3 证明恒等式：

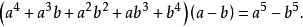
**解：**先按a的降幂、b的升幂排列。用分离系数法，最后结果中乘积的最高次项的次数是5。

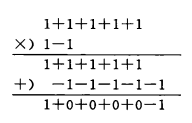
所以

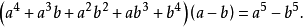
本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所