传递关系(transitive relation)是一种特殊的关系,指由甲、乙和乙、丙都有,可推知甲、丙也有的那种关系。集合A上的二元关系R,对任何a,b,c∈A,当aRb,bRc时,有aRc,用符号表示:R是A上的传递关系⇔∀a∀b∀c(a∈A∧b∈A∧c∈A∧aRb∧bRc→aRc)。当A上的R是传递关系时,称R在A上是传递的,或说A上的关系R有传递性。例如,实数集中的小于关系与不小于关系都是传递的;而人群中的同学关系是不传递的。若R在A上是传递的,则R°R⊆R;反之,如R°R⊆R,则R在A上是传递的。一个反自反的传递关系是不对称的,一个反自反的对称非空关系不是传递关系1。
基本介绍定义令R是A上的二元关系,对于A中任意的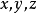 ,若
,若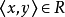 ,且
,且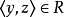 ,则
,则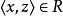 ,则称R具有传递性(或称R是传递关系)。
,则称R具有传递性(或称R是传递关系)。
R是A上的传递关系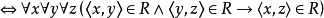 2。
2。
例题解析【例1】设A={1,2,3,4},下列几个是A 上的二元关系。
R1={,,,,,,};
R2={,,};
R3={,,,,,,,};
R4={,,,,,};
R5=(,,,,,,,,,};
R6={}。
其中,哪些是传递关系?
解: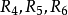 是传递的。对这些关系可以证明,若
是传递的。对这些关系可以证明,若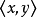 和
和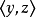 属于一个关系,则
属于一个关系,则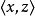 也属于这个关系,例如
也属于这个关系,例如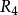 传递的,因为
传递的,因为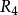 中只有和,和,和以及和是这样的有序对,而,和属于
中只有和,和,和以及和是这样的有序对,而,和属于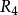 。
。
同理可证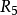 是传递的。
是传递的。
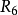 虽然只有一个序对,但它没有违反传递性的规则,故也是传递的。
虽然只有一个序对,但它没有违反传递性的规则,故也是传递的。
 不是传递的。因为
不是传递的。因为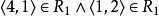 ,
,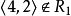 。
。
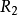 不是传递的,因为
不是传递的,因为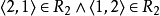 而
而 。
。
 不是传递的,因为
不是传递的,因为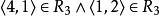 ,而
,而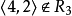 。
。
传递关系在关系图上特征表现为如果结点u到v有边,v到w有边,则必有从u到w的边。
传递关系的性质设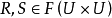 ,则有:
,则有:
(1)若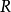 是传递的。则
是传递的。则 。
。
(2)若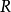 是传递的,则
是传递的,则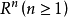 是传递的。
是传递的。
(3)若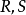 是传递的,则
是传递的,则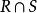 是传递的。
是传递的。
关系的判断综上所述。判断一个A上的二元关系具有哪些性质。可以从定义出发,或者观察关系的关系图和关系矩阵。对于一些简单的特征明显的关系是容易判断的,然而如何判断任意一个关系具有哪些性质呢?下面给出判断的形式化表示。
定理1 设R是A上的二元关系,则
(1) R是自反关系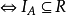 。
。
(2) R是反自反关系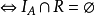 。
。
(3)R是对称关系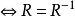 。
。
(4)R是反对称关系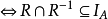 。
。
(5)R是传递关系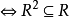 。
。
例2利用定理1判断例1中各关系具有的性质。
解: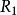 5种性质都不具备,原因如下。
5种性质都不具备,原因如下。
(1)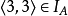 ,而
,而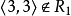 ,所以
,所以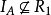 ,故
,故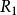 不具有自反性。
不具有自反性。
(2)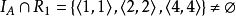 ,故
,故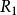 不具有自反性。
不具有自反性。
(3) 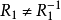 ,故
,故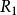 不是对称的。
不是对称的。
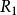 (4)
(4)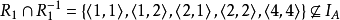 ,故不是反对称的。
,故不是反对称的。
(5) 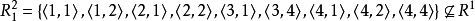 ,故
,故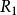 不是传递的。
不是传递的。
同理可以判断:
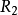 是对称的,不是自反的、反自反的、反对称的、传递的;
是对称的,不是自反的、反自反的、反对称的、传递的;
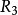 是自反的、对称的,不是反自反的、反对称的、传递的;
是自反的、对称的,不是反自反的、反对称的、传递的;
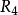 是反自反的、反对称的、传递的,不是自反的、对称的;
是反自反的、反对称的、传递的,不是自反的、对称的;
 是自反的、反对称的、传递的,不是反自反的、对称的;
是自反的、反对称的、传递的,不是反自反的、对称的;
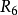 是反自反的、反对称的、传递的,不是自反的、对称的2。
是反自反的、反对称的、传递的,不是自反的、对称的2。
相关概念二元关系设A,B是两个集合,R是A×B的任意一个子集,即
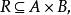 则称R为从集合A到集合B的一个二元关系,简称为从A到B的一个二元关系。
则称R为从集合A到集合B的一个二元关系,简称为从A到B的一个二元关系。
若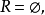 称R为空关系。
称R为空关系。
若R=A×B,称为全关系。
当A=B时,称二元关系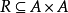 为A上的二元关系。
为A上的二元关系。
当A=B时,记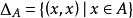 称之为A上的恒等关系。
称之为A上的恒等关系。
自反关系与反自反关系定义1令R是A上的二元关系,若对于A中的每个 都有
都有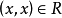 ,则称R具有自反性(或称R是自反关系)。
,则称R具有自反性(或称R是自反关系)。
即R是A上的自反关系 。
。
定义2令R是A上的二元关系,若不存在A中的 ,使得
,使得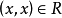 ,则称R具有反自反性(或称R是反自反关系)。
,则称R具有反自反性(或称R是反自反关系)。
即R是A上的反自反关系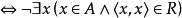 。
。
自反的关系亦称“具有反身性的关系”。对于类K中一个确定的关系R来说,若类K中任意的个体和它自身都具有关系R,则称关系R在类K中为自反的关系。若类K中没有一个个体和它自己具有关系R,则称关系R在类K中为反自反的关系。若类K中有的个体和它自己具有关系R,而有的个体和它自己不具有关系R,则称关系R在类K中为非自反的****关系。例如,设类K为实数域,则等于关系“=”是自反的关系,大于关系“>”,小于关系“




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国