组合最优化又称组合规划,是在给定有限集的所有具备某些特性的子集中,按某种目标找出一个最优子集的一类数学规划。初期,它所研究的问题,如广播网的设计、旅游路线的安排、课程表的制订等,都是网络上的一些极值问题。后来,对这些问题进行概括和抽象,在理论上研究了拟阵中一些更一般的组合最优化问题及算法。主要研究内容有:线性组合最优化问题;网络上的最优化问题;独立系统和拟阵,拟阵是组合优化中一个基本而重要的概念,许多组合问题都可化为拟阵问题。贪心算法是求拟阵的最优独立集的简单算法;交错链算法是求解最优交问题的基本算法。对问题算法的分类也是一类主要研究内容。某些算法具有多项式时间复杂度,如贪心算法、交错链算法,称之为多项式时间算法,能用多项式算法求解的问题为P问题。还有一类问题从求解的计算量角度看有如下共性:①它们都未找到多项式算法。②若对其中的某一个问题存在多项式算法,则这一类的所有问题也都有多项式算法。这些问题组成的等价类称为NP完备问题,如装箱问题、推销员问题等。人们在求解这类问题时,往往采用“启发式”算法,不能保证求得最优解,但常常能求得较好的近似解1。
基本介绍组合最优化是通过对数学方法的研究去寻找处理离散事件的最优编排、分组、次序或筛选等问题的优化方法。组合最优化实际上就是从有限个离散状态中选取最好的状态。这种优化问题一般可以描述为
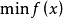 ←目标函数
←目标函数
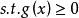 ←约束条件
←约束条件
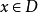 ←定义域
←定义域
我们称这种优化问题为组合优化问题。现实中的大量优化问题就是从有限个状态中选取最好的状态,因此,大量的实际优化问题是组合优化问题。最优化问题一般分为两大类:一类是具有连续型的变量,另一类是具有离散型的变量,后一类被称为组合最优化,组合优化问题有时又称为离散优化(Discrete Optimization)问题。
实际上,上述组合优化问题是一个规划问题。解决这类优化问题的方法有各种规划(线性、非线性、目标、整数、随机、模糊)、遗传算法、退火算法、神经网络、搜索算法**、拉格朗日松弛算法**等。
一个组合最优化问题可以用3个参 表示,其中D表示决策变量的定义域,F表示可行解区域,F中的任何一个元素称为该问题的可行解,
表示,其中D表示决策变量的定义域,F表示可行解区域,F中的任何一个元素称为该问题的可行解,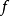 表示目
表示目
标函数。组合最优化的特点就是可行解集合为有限点集。由直观可知,只要将定义域D中的有限个点逐一判别是否满足约束,并比较目标函数的大小,就可以得到该问题的最优解,这就是枚举法。对于某些优化问题可以通过枚举法得到最优解,这在问题规模较小时是十分有效的,也是非常全面的。但对于复杂的问题,枚举法显然是无法接受的。每一个组合最优化问题都可以通过枚举的方法求得最优解,然而枚举是以时间为代价的,有的枚举时间还可以接受,有的则不可能接受。
有的优化问题是有实时性要求的,如作战决策、天气预报等。因此,在这种情况下,对于优化问题还要附加时间性要求。
比如典型的旅行商(Traveling Salesman Problem,TSP)问题,若采用枚举法,则计算时间如表1所列。
|| || 表1 旅行商问题
对于这种问题至今为止还没有找到一种求最优解的算法,而这些组合最优化问题又有非常强的实际应用背景。因此,人们不得不尝试采用一些并不一定能保证可以求得最优解的算法来求解组合最优化问题,我们称之为启发式算法。
组合最优化包含了许多常用的但一般很难处理的著名问题,像最短路问题、最小树问题、匹配问题和旅行售货员问题,也都属于组合最优化问题。下面介绍一些典型问题并介绍几种基本方法。
背包问题和Greedy算法(贪婪算法)有n件东西重量为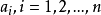 ,价格为
,价格为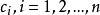 ,要求从中选出若干件装入背包,即使总重量不超过M,又使总价值最大。
,要求从中选出若干件装入背包,即使总重量不超过M,又使总价值最大。
Greedy算法:将比值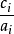 由小到大排好队逐件考虑,不超重就装入,否则放弃,考虑下一件。
由小到大排好队逐件考虑,不超重就装入,否则放弃,考虑下一件。
算法的实质就是“挑好的装,装进后就不再换出”。不过,一般这种方法不一定能求得最优解。其实背包问题是NP-Complete问题,至今没有有效解法。
匹配问题和交错链方法Greedy算法对背包问题不能保证求得最优解,但是能求得一个比较好的初始解。人们通常以它为基础再作一些调整。例如,尝试用两件东西去换1件或3件去换2件等办法来改进所求的解。交错链方法就是这种朴素思想的发展,它是组合最优化方法的核心。
下面通过匹配问题来说明交错链方法。
有n个工人和n项工作,每个人只能适应其中某几项工作。要求寻找一种分配方式,使得尽可能多的人分配到适应的工作岗位上。
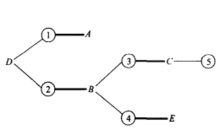
例如,有5个工人:A、B、C、D、E,5项工作1,2,3,4,5,各工人与各工作之间的适应关系如图1所示。图中有线段相连表示适应。例如,A适应于1和2,问最多能同时安排几个人的工作?
|| ||
从图上看,是要求利用线段将图中的端点一一配对,且希望配得对数越多越好。这就是图论中最大匹配问题。可见,所谓匹配就是无公共顶点的边所组成的集合。
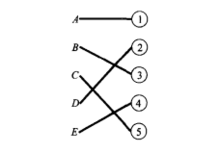
首先,通过直觉观察,求出一个较好的初始匹配方案。在图中用粗线段标出,如图2所示。这时已连上粗线段的点称为已盖点,尚未连粗线的点称为未盖点,图上的一条路,若路上的线段粗细交错,则称其为交错链,如图3所示。称连接两个未盖点的交错链为增广链。对于增广链,细线段比粗线段多一条。对给定的匹配方案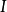 ,假若存在一增广链S,那么只要把路S上的细线和粗线交换一下,便可得到多安排一个人的新匹配方案
,假若存在一增广链S,那么只要把路S上的细线和粗线交换一下,便可得到多安排一个人的新匹配方案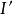 。通常用下述符号表示上述调整运算:
。通常用下述符号表示上述调整运算:
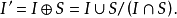 图论中有下列基本事实:
图论中有下列基本事实:
定理1 一个匹配为最大匹配的充要条件是不存在关于它的增广链。
如何寻找增广链?采用“树生长法”(或称标号法),以图2为例,开始任取一未盖点为树根,如D,从树根沿着细线生长,接着从树梢出发沿着粗线往外生长,这样交错地沿着细线和粗线继续从树梢往外延伸,直到不能再生长(如图4)。称图4是以D为根的交错树。在树的生长过程中,一旦发现除树根外,另一未盖点被长到树上,过程就可中止。这时树上连结两个未盖点的那条路,便是一条增广链。图4中D与⑤之间就是一条增广链,沿着它们调整后,可得匹配图5。
总结交错链方法的计算步骤如下:
1.任选初始的匹配图;
2.利用树生长法寻找增广链。如果找到一条增广链则转步骤3;如果所有交错树上都无增广链,则步骤终止,已找到最大匹配;
3.(调整)替换增广链上的粗线和细线,得到一个新的匹配图,然后转步骤1。交错链方法的计算量是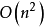 2。
2。
排序问题和分枝定界法在许多可能的顺序中找一个最优顺序,分配加上加工顺序的限制,就成排序问题。例如,A与B两车床加工n件产品,加工时间分别为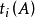 和
和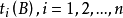 。A先加工,然后B再加工,问如何安排所用时间最少?
。A先加工,然后B再加工,问如何安排所用时间最少?
由于加工顺序是A先B后,故应尽量减少B的等待时间。因此,不难理解其最优方案应是每次从{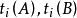 )中取出一个最小值,若它属于{
)中取出一个最小值,若它属于{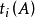 },则应排在最先加工,若属于{
},则应排在最先加工,若属于{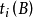 ),则应排在最后加工,然后对已确定加工顺序的数据从{
),则应排在最后加工,然后对已确定加工顺序的数据从{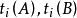 )中去掉。在余集上重复上述过程,依次排列,便得最优排序。此问题也可用动态规划的方法求解。
)中去掉。在余集上重复上述过程,依次排列,便得最优排序。此问题也可用动态规划的方法求解。
上述是2×n的同顺序排序问题,对于一般的m×n(m>3)的同顺序排序问题及不同顺序的排序问题,要用“分枝定界法”求解,现将该方法简介如下:
分枝定界法
欲求

考虑求
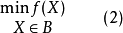
其中:要求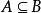 ,称式(2)为式(1)的松弛问题,它容易求解。若式(2)的最优解
,称式(2)为式(1)的松弛问题,它容易求解。若式(2)的最优解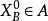 ,则
,则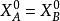 ;否则,分A为两个(或多个)子集:
;否则,分A为两个(或多个)子集: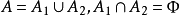 ,解相应的松弛问题:
,解相应的松弛问题: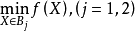 ;若
;若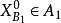 ,则
,则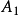 问题已解决(否则,对
问题已解决(否则,对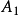 重复A的过程)。同样若
重复A的过程)。同样若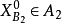 ,则
,则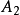 问题已解决,从而
问题已解决,从而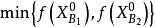 即为所求最小值。若
即为所求最小值。若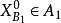 而
而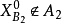 (但
(但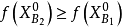 ),则
),则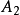 也不必考虑了;否则,对
也不必考虑了;否则,对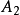 继续实行如同A的步骤,如此进行,直到求得最优值为止(
继续实行如同A的步骤,如此进行,直到求得最优值为止(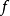 取最小的子集先考虑)。
取最小的子集先考虑)。
中国邮递员问题一个邮递员负责投递某个街区的邮件,现在需要为他设计一条最短的线路,从邮局出发,经过投递区内每条街道至少一次,最后返回邮局。一般说来,为了经过每条街道至少一次,有些街道可能需要重复通过,如果限制每条街道不得通过三次或三次以上(可以证明某段街道通过三次或三次以上的投递路线一定是可以简化的),那么所有可能的投递路线的总数就是有限的,也就是说中国邮递员问题的可行解个数是有限的,因此它是一个组合最优化问题,这个问题是我国管梅谷教授在1960年首先提出的,所以在国际上被称为“中国邮递员问题”,中国邮递员问题已被公认为重要的组合最优化问题之一。
旅行售货员问题某公司的商品推销员打算从城市1出发,走遍城市2,3,…,n,去推销商品,最后回到城市1。问如何安排他的旅行路线,使走的路线的总长度最短(有时我们加上“经过每个城市恰好一次”这样的限制),这个问题称为旅行售货员问题。
旅行售货员问题的研究已经有四十多年的历史了,是组合最优化问题中另一个重要的研究课题,比较一下旅行售货员问题和中国邮递员问题是很有趣的,它们的提法看上去很相似,但实际上有本质的区别。
最小连接问题给定n个城市。现在需要架设通讯线路,把这n个城市都连接起来,假定架设连接城市i和城市j的通讯线路所需费用为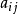 ,问应该在哪些城市之问架设线路,既能使所有城市之间都能连通,又要总的架设费用最小?这个问题等价于最小树问题3。
,问应该在哪些城市之问架设线路,既能使所有城市之间都能连通,又要总的架设费用最小?这个问题等价于最小树问题3。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国